Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài của thang là BC, khoảng cách từ chân thang đến chân tường là AC
Theo đề, ta có: BC=3,5m; AC=1,6m; AC\(\perp\)AB tại A
Ta có: ΔABC vuông tại A
=>\(cosC=\dfrac{CA}{CB}\)
=>\(cosC=\dfrac{1.6}{3.5}=\dfrac{16}{35}\)
=>\(\widehat{C}\simeq63^0\)
=>\(60^0< =\widehat{C}< =65^0\)
=>Đạt tiêu chuẩn

Bài 2
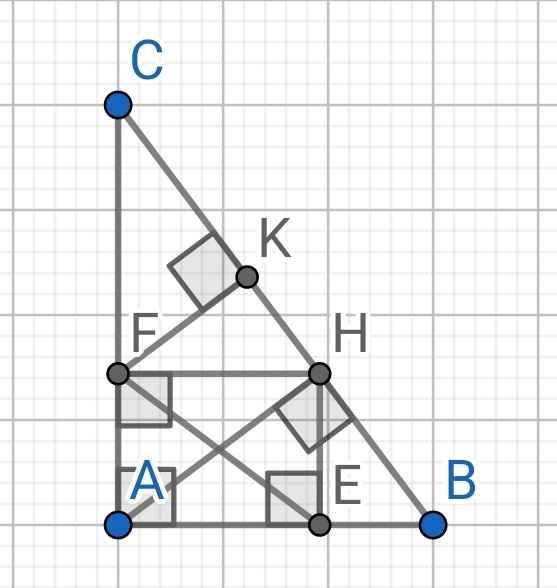 a) ∆ABC vuông tại A, AH là đường cao
a) ∆ABC vuông tại A, AH là đường cao
⇒ AH² = BH.HC
= 4.9
= 36
⇒ AH = 6 (cm)
BC = BH + HC
= 4 + 9 = 13 (cm)
∆ABC vuông tại A, AH là đường cao
⇒ AB² = BH.BC
= 4.13
= 52 (cm)
⇒ AB = 2√13 (cm)
⇒ cos ABC = AB/BC
= 2√13/13
⇒ ∠ABC ≈ 56⁰
b) ∆AHB vuông tại H, HE là đường cao
⇒ AH² = AE.AB (1)
∆AHC vuông tại H, HF là đường cao
⇒ AH² = AF.AC (2)
Từ (1) và (2) suy ra:
AE.AB + AF.AC = 2AH² (3)
Xét tứ giác AEHF có:
∠HFA = ∠FAE = ∠AEH = 90⁰ (gt)
⇒ AEHF là hình chữ nhật
⇒ AH = EF (4)
Từ (3) và (4) suy ra:
AE.AB + AF.AC = 2EF²
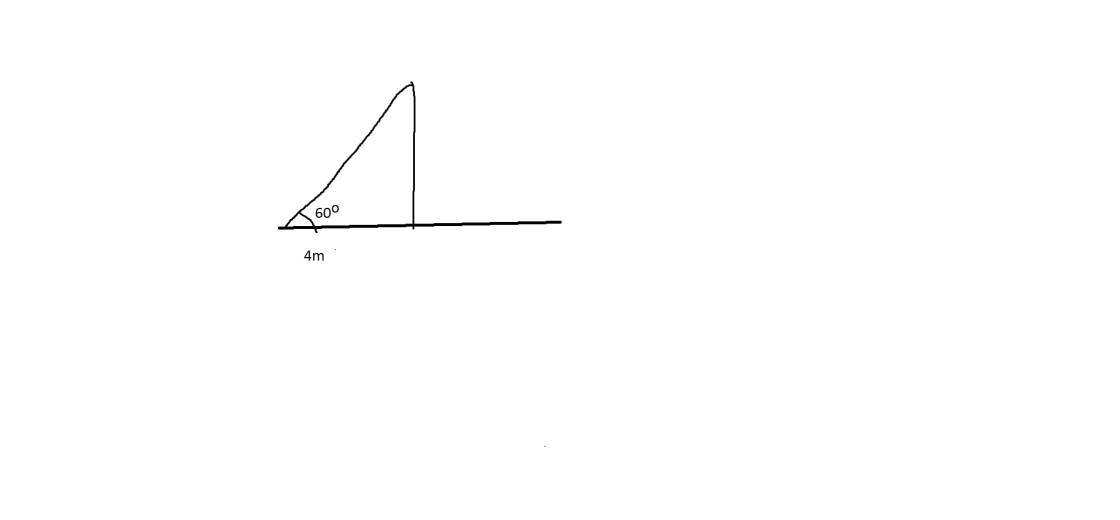
Bài 1
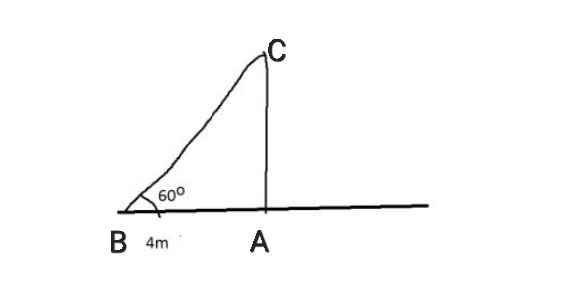 Ta có:
Ta có:
tan B = AC/AB
⇒ AC = AB . tan B
= 4 . tan60⁰
= 4√3 (m)
≈ 7 (m)

Chiều cao của cột cờ là:
\(10.5\cdot tan\left(35^045'\right)\simeq7,56\left(m\right)\)

Gọi chiều cao tháp và bóng lúc tia sáng hợp với mặt đất góc 24 độ là x, y thì ta có hệ
\(\hept{\begin{cases}x=y.tan24^o\\x=\left(y+8,5\right).tan20^o\end{cases}}\)

chân thang cần đặt cách chân tường 1 đoạn là:6*cos65=2.54 cm

Gọi c là chu vi Trái đất, góc ∠AOS = α. Ta có:

Vì các tia sáng chiếu thẳng đứng nên BC // SO do đó:
∠AOS = ∠ACB (so le trong)
Trong tam giác ABC vuông tại A có:
![]()
Vì ∠AOS = ∠ACB nên α = 7,07o
Vậy chu vi Trái đất là:
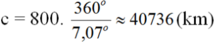

Gọi c là chu vi Trái đất, góc ∠AOS = α. Ta có:
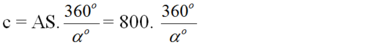
Vì các tia sáng chiếu thẳng đứng nên BC // SO do đó:
∠AOS = ∠ACB (so le trong)
Trong tam giác ABC vuông tại A có:
![]()
Vì ∠AOS = ∠ACB nên α = 7 , 07 °
Vậy chu vi Trái đất là:

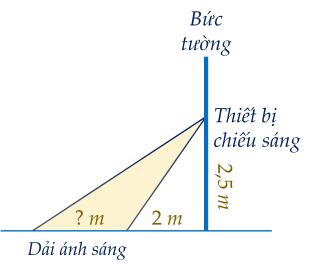


∆ABC vuông tại A
⇒ tanC = AB : AC = 2 : 2,5 = 0,8
⇒ C ≈ 39⁰
⇒ ACD = 20⁰ + 39⁰ = 59⁰
∆ACD vuông tại A
⇒ tanACD = AD : AC
⇒ AD = AC.tanACD
= 2,5.tan59⁰
≈ 4,2 (m)
Độ dài vùng được chiếu sáng trên mặt đất:
BD = AD - AB = 4,2 - 2 = 2,2 (m)