S=1/2^2+1/3^2+1/4^2+....+1/9^2.Chứng minh rằng 2/5 < S <8/9

K

Khách

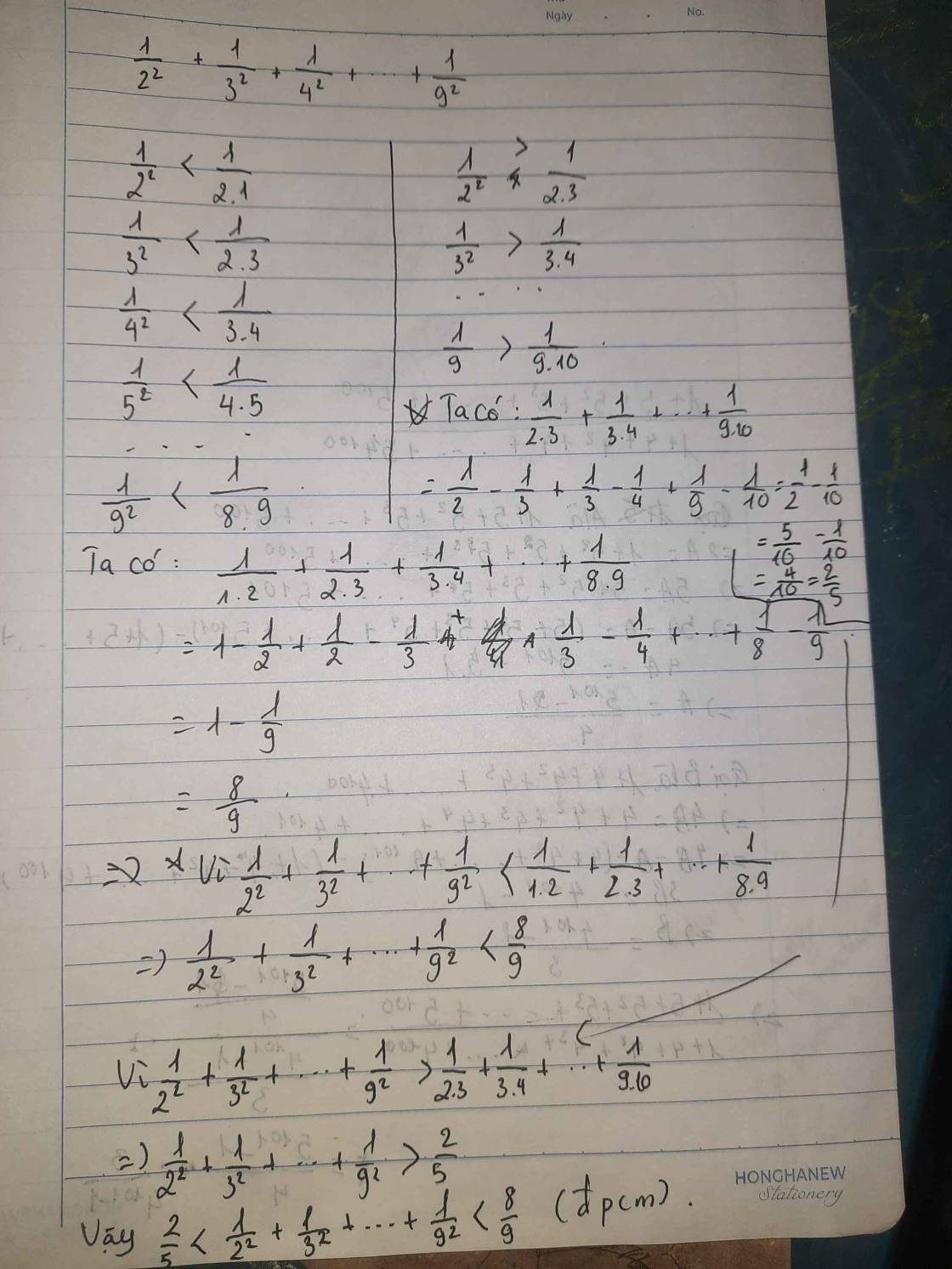
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PN

Phong Ngô

28 tháng 10 2023 - olm

S=1/2^2+1/3^2+1/4^2+....+1/9^2.Chứng minh rằng 2/5 < S <8/9

1

PT

Phạm Thanh Thảo

22 tháng 11 2023

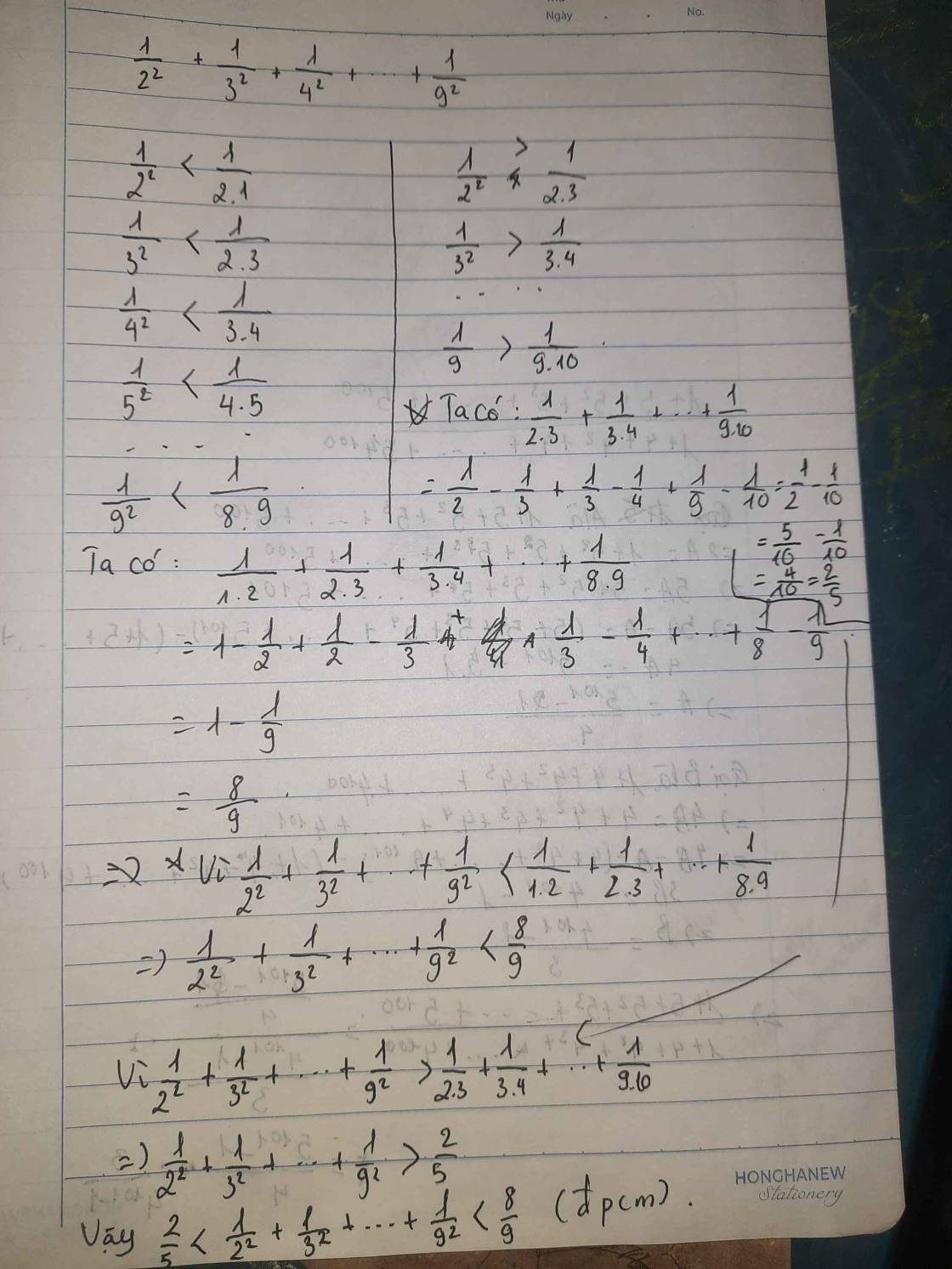
loading...

Các câu hỏi dưới đây có thể giống với câu hỏi trên

NY

Nakame Yuuki

5 tháng 11 2015 - olm

Cho \(S=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+....+\frac{1}{9^2}\)

CMR : 2/5 < S < 8/9

0

NH

nguyễn hải bình

31 tháng 7 2015 - olm

Cho S = 1/5^2 + 1/9^2 +.....+ 1/409^2.

CHỨNG MINH S<1/12

khẩn cấp!!!!!!!!!!!

0

KQ

Kiều Quốc Nam

16 tháng 10 2016 - olm

Cho \(A=\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{9^2}\)Chứng minh \(\frac{2}{5}< A< \frac{8}{9}\)

1

NP

Nguyễn Phương Linh

16 tháng 10 2016

\(A< \frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{8.9}\)

\(\Rightarrow A< 1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{8}-\frac{1}{9}\)

\(\Rightarrow A< 1-\frac{1}{9}=\frac{8}{9}\)(1)

Lại có: \(A>\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}\)

\(\Rightarrow A>\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}\)

\(A>\frac{1}{2}-\frac{1}{10}=\frac{2}{5}\)(2)

Từ (1) và (2), suy ra: \(\frac{2}{5}< A< \frac{8}{9}\)

PN

phạm ngọc thái

24 tháng 2 2019 - olm

Chứng minh S=\(\frac{3}{1^2.2^2}+\frac{5}{2^2.3^2}+...+\frac{19}{9^2.10^2}\)<1

1

ZC

zZz Cool Kid_new zZz

24 tháng 2 2019

\(S=\frac{3}{1^2\cdot2^2}+\frac{5}{2^2\cdot3^2}+.....+\frac{19}{9^2\cdot10^2}\)

\(\Rightarrow S=\frac{3}{1\cdot4}+\frac{5}{4\cdot9}+....+\frac{19}{81\cdot100}\)

\(\Rightarrow S=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{9}+....+\frac{1}{81}-\frac{1}{100}\)

\(\Rightarrow S=1-\frac{1}{100}=\frac{99}{100}< 1\left(ĐPCM\right)\)

TT

thanh tam tran

12 tháng 9 2016 - olm

chứng minh rằng S=1/1^2+1/2^2+1/3^2+1/4^2+...+1/100^2<12/3

0

QQ

Quách Quỳnh Bảo Ngọc

29 tháng 8 2015 - olm

Chứng minh rằng:

a) A=1/3+1/(3^2)+1/(3^3)+...+1/(3^99)<1/2

b) B=3/(1^2*2^2)+5/(2^2*3^2)+7/(3^2*4^2)+...+19/(9^2*10^2)<1

c) C=1/3+2/(3^2)+3/(3^3)+4/(3^4)+...+100/(3^100)<3/4

0

K

kikyou

4 tháng 7 2016 - olm

S=(1+1/3).(1+1/3^2).(1+1/3^4)......(1+1/3^500)

chứng minh rằng: S<3/2

0

VH

Vũ Huyền

5 tháng 8 2015 - olm

a) chứng minh rằng 1/2²+ 1/3²+ 1/4²+ ...... + 1/2008²< 1

b) cho A= 100²⁰⁰⁷+ 1/ 100²⁰⁰⁸ +1; B= 100²⁰⁰⁶+ 1/ 100²⁰⁰⁷+1. hãy so sánh A và B?

c) S= 1/31+1/32+...+1/60. chứng minh: 3/5 < S < 4/5

0

NP

Nguyễn phan Thủy ngân

11 tháng 12 2016 - olm

F = 1/2²+ 1/3²+...........+ 1/9² chứng minh 2/5<F<8/9

0