Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ABCD là hình chữ nhật
=>\(AC^2=AD^2+DC^2\)
=>\(AC=\sqrt{8^2+15^2}=17\left(cm\right)\)
b: ΔDAC vuông tại D có DM là đường cao
nên DM^2=MA*MC; DM*AC=DA*DC
=>DM*17=8*15
=>DM=120/17(cm)
c: Xét ΔMAN vuông tại M và ΔMIC vuông tại M có
góc MAN=góc MIC
Do đó: ΔMAN đồng dạng với ΔMIC
=>MA/MI=MN/MC
=>MA*MC=MI*MN=MD^2
Cái quan trọng là câu d ý bạn mấy câu đó mình làm được hết r

1.
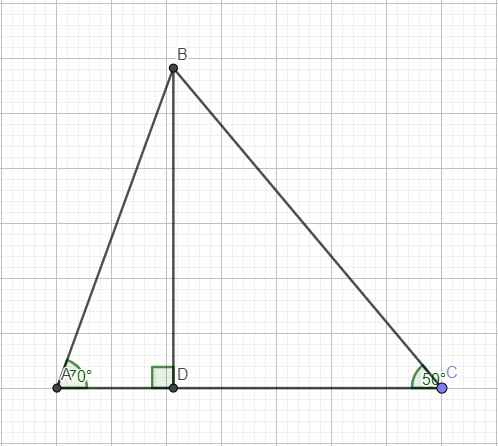
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)

AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm

[ACD] = [ABCD] - [ABC] = 35,3554 cm2
kẻ BH _|_ AC ; DK_|_ AC cắt MN tại P
=> \(k=\frac{DP}{DK}=\frac{DP}{DK}-1+1=\frac{PK}{DK}+1=\frac{BH}{DK}+1=\frac{\left[ABC\right]}{\left[ACD\right]}+1=1,4399978504\)
[DMN]=k2 .[ADC] = .....tự tính nhé