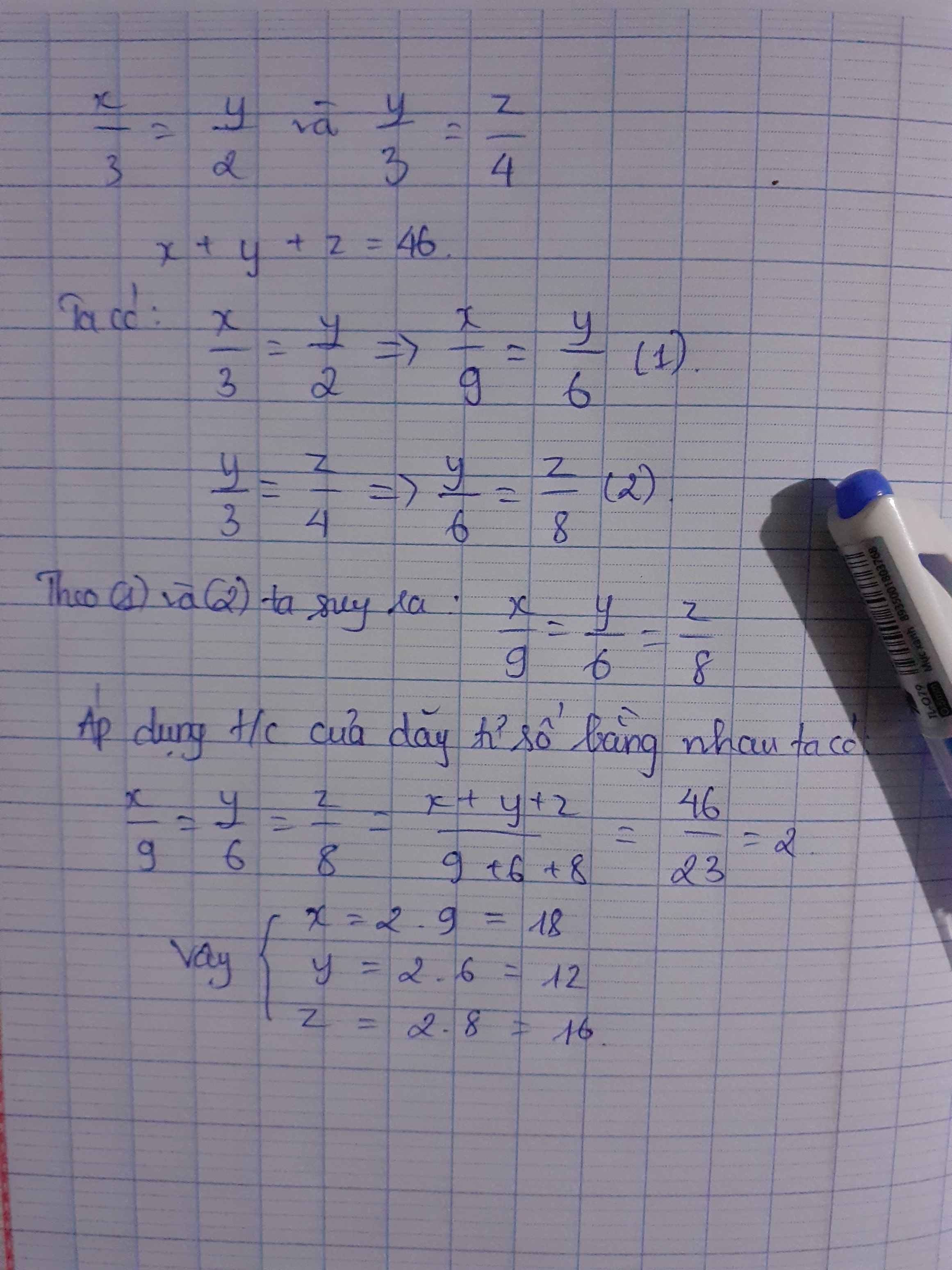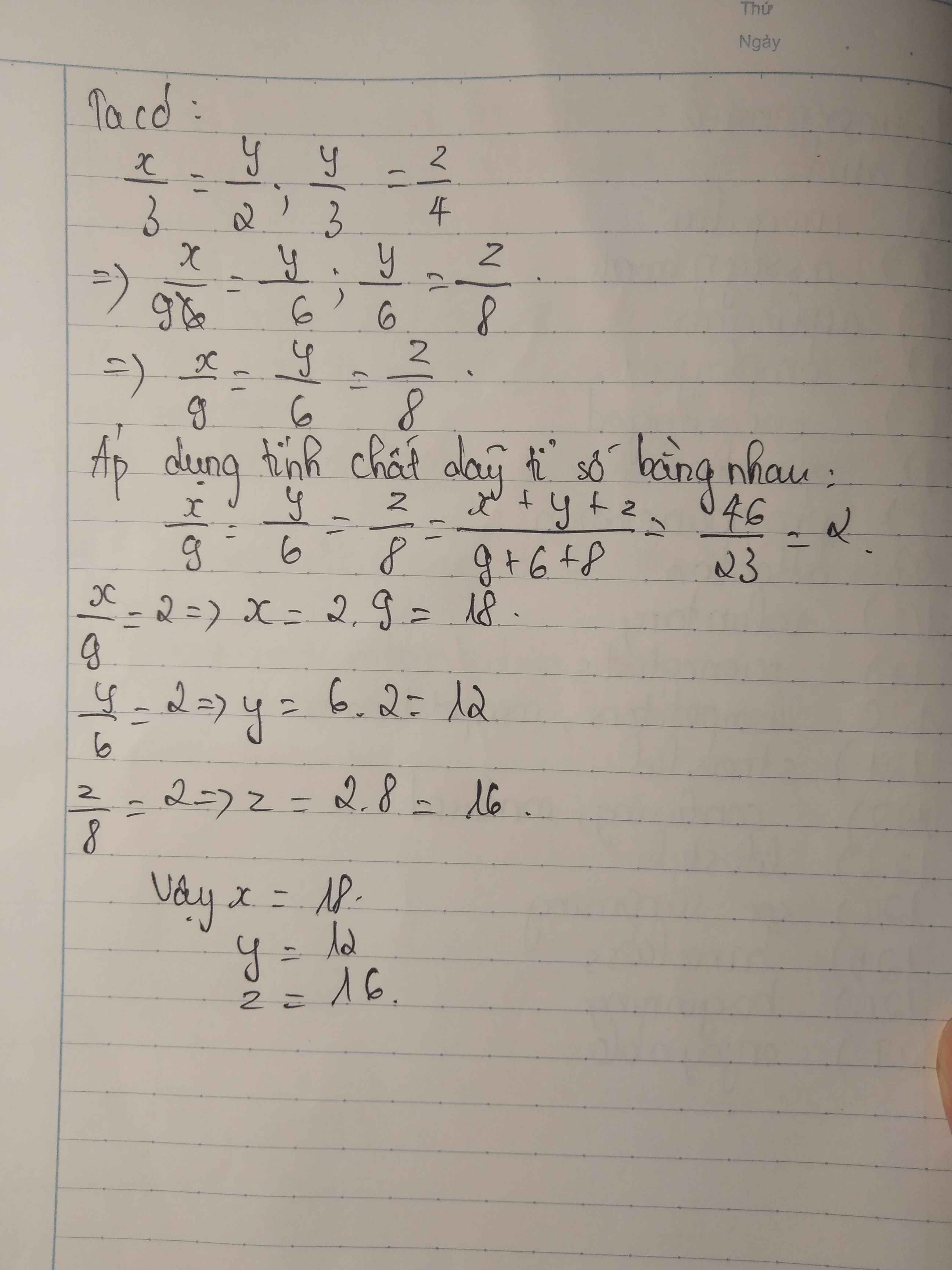Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{x}{3}=\frac{y}{2}\Rightarrow\frac{x}{9}=\frac{y}{6}\)(1)
\(\frac{y}{3}=\frac{z}{4}\Rightarrow\frac{y}{6}=\frac{z}{8}\)(2)
Từ (1) và (2) => \(\frac{x}{9}=\frac{y}{6}=\frac{z}{8}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{9}=\frac{y}{6}=\frac{z}{8}=\frac{x+y+z}{9+6+8}=\frac{46}{23}=2\)
=>x=2.9=18
y=2.6=12
z=2.8=16
Vậy...

Áp dụng t/c dtsbn:
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{z}{11}=\dfrac{x+y+z}{5+7+11}=\dfrac{-46}{23}=-2\)
\(\Rightarrow\left\{{}\begin{matrix}x=\left(-2\right).5=-10\\y=\left(-2\right).7=-14\\z=\left(-2\right).11=-22\end{matrix}\right.\)

\(\frac{x}{y}=\frac{2}{3}\Rightarrow\frac{x}{2}=\frac{y}{3}\)
\(\frac{y}{z}=\frac{5}{7}\Rightarrow\frac{y}{5}=\frac{z}{7}\)
Ta có:
\(\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x+y+z}{10+15+21}=\frac{46}{46}=1\)
\(\frac{x}{10}=1\Rightarrow x=10\)
\(\frac{y}{15}=1\Rightarrow y=15\)
\(\frac{z}{21}=1\Rightarrow z=21\)
\(\Rightarrow x+y-z=10+15-21=4\)
Vậy x + y - z = 4
Ta có: \(\frac{x}{y}=\frac{2}{3}\Rightarrow\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{10}=\frac{y}{15}\)
\(\frac{y}{z}=\frac{5}{7}\Rightarrow\frac{y}{5}=\frac{z}{7}\Rightarrow\frac{y}{15}=\frac{z}{21}\)
\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{21}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{21}=\frac{x+y+z}{10+15+21}=\frac{46}{46}=1\)
\(\Rightarrow\hept{\begin{cases}x=10\\y=15\\z=21\end{cases}}\)
\(\Rightarrow x+y-z=10+15-21=4\)
Vậy...


Ta có: \(\frac{x}{2}=\frac{y}{3}\) và\(\frac{y}{5}=\frac{z}{6}\)và \(2x-y+z=46\)
\(\Rightarrow\frac{x}{10}=\frac{y}{15}=\frac{z}{18}\)và \(2x-y+z=46\)
\(\Rightarrow\frac{2x}{20}=\frac{y}{15}=\frac{z}{18}\)và\(2x-y+z=46\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{2x}{20}=\frac{y}{15}=\frac{z}{18}=\frac{2x-y+z}{20-15+18}=\frac{46}{23}=2\)
Ta có: \(\frac{x}{10}=\frac{2x}{20}=2\Rightarrow x=2.10=20\)
\(\frac{y}{15}=2\Rightarrow y=2.15=30\)
\(\frac{z}{18}=2\Rightarrow z=2.18=36\)
Vậy:\(x=20;y=30\)và\(z=36\)

Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{3}\\\dfrac{y}{3}=\dfrac{z}{4}\end{matrix}\right.\Rightarrow\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+y+z}{2+3+4}=\dfrac{46}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2.46}{9}=\dfrac{92}{9}\\y=\dfrac{3.46}{9}=\dfrac{46}{3}\\z=\dfrac{4.46}{9}=\dfrac{184}{9}\end{matrix}\right.\)
Vậy ...
P/s: Đề đúng không nhỉ?

1)
\(3x=2y=z\)
\(\Rightarrow\frac{3x}{6}=\frac{2y}{6}=\frac{z}{6}\)
\(\Rightarrow\frac{x}{2}=\frac{y}{3}=\frac{z}{6}\)
Áp dụng tc của dãy tỉ số bằng nhau Ta có
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{6}=\frac{x+y+z}{2+3+6}=\frac{99}{11}=9\)
\(\Rightarrow\begin{cases}x=18\\y=26\\z=54\end{cases}\)
2)
\(6x=10y=14z\)
\(\Rightarrow\frac{6x}{210}=\frac{10y}{210}=\frac{14z}{210}\)
\(\Rightarrow\frac{x}{35}=\frac{y}{21}=\frac{z}{15}\)
Áp dụng tc của dãy tỉ số bằng nhau Ta có
\(\frac{x}{35}=\frac{y}{21}=\frac{z}{15}=\frac{x+y+z}{35+21+15}=\frac{46}{71}\)
\(\Rightarrow\begin{cases}x=\frac{1610}{71}\\y=\frac{966}{71}\\z=\frac{690}{71}\end{cases}\)

Ta có: `x/3=y/2 -> x/9=y/6`
`y/3=z/4 -> y/6=z/8`
Từ `2` điều trên `-> x/9=y/6=z/8`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/9=y/6=z/8=(x+y+z)/(9+6+8)=46/23=2`
`-> x/9=y/6=z/8=2`
`-> x=2*9=18, y=2*6=12, z=2*8=16.`