
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(z^2=\left(x+y\right)^2\le\left(1^2+1^2\right)\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\frac{z^2}{2}\)
Min= \(\frac{z^2}{2}\) khi x=y=x/2

→Tìm max:
Ta có bđt sau với mọi x,y: xy ≤ (x² + y²)/2 (đẳng thức xảy ra khi x = y)
kết hợp với giả thiết: x² + y² = 4 + xy ≤ 4 + (x² + y²)/2
=> P ≤ 4 + P/2
<=> P ≤ 8
Max P = 8 xảy ra khi x = y và x² + y² - xy = 4 <=> x = y = 2 hoặc x = y = - 2 •
→ Tìm min:
P = x² + y² = 4 + xy
+ Nếu xy ≥ 0 thì P ≥ 4
+ Nếu xy < 0: không mất tính tổng quát giả sử x > 0; y < 0
để tiện cho việc cm, đặt y = - z với z > 0
Ta có: P/4 = (x² + y²)/4 = (x² + y²)/(x² + y² - xy)
= 1 + xy/(x² + y² + xy) = 1 - zx/(x² + z² + zx)
mặt khác:
x² + z² ≥ 2zx
=> x² + z² + zx ≥ 3zx
=> zx/(x² + z² + zx) ≤ 1/3 (vì zx > 0)
=> P/4 = 1 - zx/(x² + z² + zx) ≥ 1 - 1/3 = 2/3
=> P ≥ 8/3
Min P = 8/3 xảy ra khi z = x = - y; x² + y² - xy = 4 <=> x = 2/√3; y = -2/√3 hoặc x = -2/√3; y = 2/√3

ta có: \(2P=2x^2-2x\sqrt{y}+2x+2y-2\sqrt{y}+2\)
\(2P=\left(x^2-2x\sqrt{y}+y\right)+\left(x^2+2x+1\right)+\left(y-2\sqrt{y}+1\right)\)
\(2P=\left(x-\sqrt{y}\right)^2+\left(x+1\right)^2+\left(\sqrt{y}-1\right)^2\ge0\forall x,y\)
\(\Rightarrow P\ge0\forall x,y\)
dấu = xảy ra khi \(\left\{\begin{matrix}x=\sqrt{y}\\x=-1\\\sqrt{y}=1\end{matrix}\right.\)(có gì đó sai sai)

\(A=\frac{2x+3y}{2x+y+2}\)
\(\Leftrightarrow A\left(2x+y+2\right)=2x+3y\)
\(\Leftrightarrow2A=2x\left(1-A\right)+y\left(3-A\right)\)
\(\Leftrightarrow\left(2A\right)^2=\left(2x\left(1-A\right)+y\left(3-A\right)\right)^2\le\left(4x^2+y^2\right)\left(\left(1-A\right)^2+\left(3-A\right)^2\right)\)
\(\Leftrightarrow\left(2A\right)^2\le\left(\left(1-A\right)^2+\left(3-A\right)^2\right)\)
\(\Leftrightarrow-5\le A\le1\)



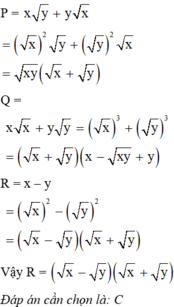
\(A=xx+yy=x^2+y^2\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(1\cdot x+1\cdot y\right)^2=4\)
\(\Rightarrow2\left(x^2+y^2\right)\ge4\)
\(\Rightarrow A\ge2\)
Dấu "=" xảy ra khi \(\left\{\begin{matrix}x+y=2\\x=y\end{matrix}\right.\)\(\Rightarrow x=y=1\)
en cam on