Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác OBDC có
\(\widehat{OBD}+\widehat{OCD}=180^0\)
Do đó: OBDC là tứ giác nội tiếp
b: Xét ΔEBA và ΔECB có
\(\widehat{E}\) chung
\(\widehat{EAB}=\widehat{EBC}\)
Do đó: ΔEBA\(\sim\)ΔECB
Suy ra: EB/EC=EA/EB
hay \(EB^2=EC\cdot EA\)

15.
Ta có \(a+b+c+ab+bc+ac=6\)
Mà \(ab+bc+ac\le\left(a+b+c\right)^2\)
=> \(\left(a+b+c\right)^2+\left(a+b+c\right)-6\ge0\)
=> \(a+b+c\ge3\)
\(A=\frac{a^4}{ab}+\frac{b^4}{bc}+\frac{c^4}{ac}\ge\frac{\left(a^2+b^2+c^2\right)^2}{ab+bc+ac}\ge a^2+b^2+c^2\ge\frac{1}{3}\left(a+b+c\right)^2\ge3\)(ĐPCM)
Bài 18, Đặt \(\left(a^2-bc;b^2-ca;c^2-ab\right)\rightarrow\left(x;y;z\right)\) thì bđt trở thành
\(x^3+y^3+z^3\ge3xyz\)
\(\Leftrightarrow x^3+y^3+z^3-3xyz\ge0\)
\(\Leftrightarrow\left(x+y+z\right)\left(x^2+y^2+z^2-xy-yz-zx\right)\ge0\)
\(\Leftrightarrow\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\right]\ge0\)
Vì \(\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\ge0\)nên ta đi chứng minh \(x+y+z\ge0\)
Thật vậy \(x+y+z=a^2-bc+b^2-ca+c^2-ab\)
\(=\frac{1}{2}\left[\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2\right]\ge0\)(đúng)
Tóm lại bđt được chứng minh
Dấu "=": tại a=b=c

Q=20-/3-x/ lớn nhất khi /3-x/ nhỏ nhất
nên /3-x/=0(vì /3-x/ luôn >=0 dấu)
3-x=0
x=3
D=4/\x-2\+2 lớn nhất khi và chỉ khi \x-2\+2 nhỏ nhất,khác 0 và lớn hơn=2(vì \x-2\ luôn EN)
nên \x-2\+2=2
\x-2\=0
x-2=0
x=2
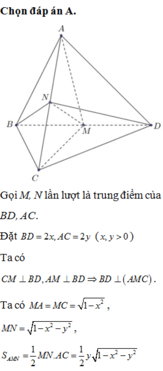
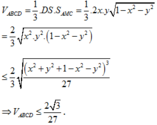

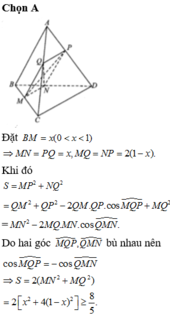

Đáp án A
Lại có I B = A B 2 - A I 2 = 1 - x 2 4 ,với AC = BD = x.
Và I H = I B 2 - B H 2 = 1 - x 2 4 - x 2 4 = 1 - x 2 2
Diện tích tam giác IBD là S ∆ I B D = 1 2 I H . B D = x 2 1 - x 2 2
Suy ra V A B C D = 2 V I . B C D = 2 3 I C . S I B D = x 3 . x 2 1 - x 2 2 = x 2 6 1 - x 2 2
Xét hàm số f x = x 2 2 - x 2 → m a x f x = 4 6 9
Vậy thể tích lớn nhất là V m a x = 4 6 9 : 6 2 = 2 3 27