
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án A
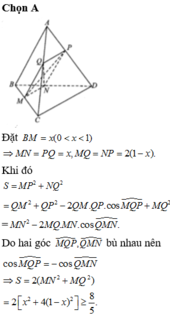
Giả sử tứ diện ABCD có AB;AC'AD đội một vuông góc ⇒ V A B C D = A B . A C . A D 6
Khi đó tứ diện MNPQ có MN;MP;MQ đội một vuông góc ⇒ V M . N P Q = M N . M P . M Q 6
Ta chứng minh được M N A B + M P A C + M Q A D = 1 ( dựa vào định lý Thalet), khi đó
M N . M P . M Q = A B . A C . A D . M N A B . M P A C . M Q A D ≤ A B . A C . A D . M N A B + M P A C + M Q A D 3 27 = A B . A C . A D 27
Vậy V M . N P Q = M N . M P . M Q 6 ≤ 1 27 . A B . A C . A D 6 = V 27 → V max = V 27

Đáp án A
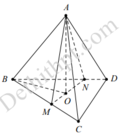
Gọi O là tâm của tam giác B C D ⇒ O A ⊥ B C D
Mà A M N ⊥ B C D suy ra MN luôn đi qua điểm O.
Đặt B M = x , B N = y ⇒ S Δ B M N = 1 2 . B M . B N . sin M B N ^ = 3 4 x y .
Tam giác ABO vuông tại O
Suy ra thể tích tứ diện ABMN là V = 1 3 . O A . S Δ B M N = 2 12 x y .
Mà MN đi qua trọng tâm của Δ B C D ⇒ 3 x y = x + y .
Do đó:
x y ≤ x + y 2 4 = 9 x y 2 4 ⇔ 1 2 ≥ x y ≥ 4 9 → V 1 = 2 24 ; V 2 = 2 27 .
Vậy V 1 + V 2 = 17 2 216 .