Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y' = f'(x)
Nếu y' > 0, ∀x ∈ (a,b) hàm số đồng biến trên khoảng (a; b)
Nếu y' < 0, ∀x ∈ (a,b) hàm số f(x) nghịch biến trên khoảng (a; b)
Nếu y' = 0, ∀x ∈ (a,b) hàm số f(x) không đổi trên khoảng (a; b)
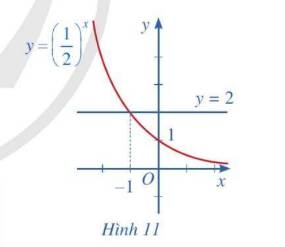
Do \(\dfrac{1}{2}< 1\) ⇒ Hàm số \(y=\left(\dfrac{1}{2}\right)^x\) nghịch biến trên R.
\(\left(\dfrac{1}{2}\right)^x>2\\ \Rightarrow x< log_{\dfrac{1}{2}}2\\ \Rightarrow x< -1\)

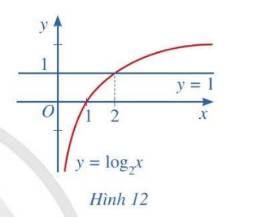
Do 2 > 1 ⇒ hàm số y = log2x đồng biến trên D = \(\left(0;+\infty\right)\)
\(log_2x>1\\ \Rightarrow x>2\)

ĐKXĐ: \(x^2-6x+5>=0\)
=>(x-1)(x-5)>=0
TH1: \(\left\{{}\begin{matrix}x-1>=0\\x-5>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=1\\x>=5\end{matrix}\right.\Leftrightarrow x>=5\)
TH2: \(\left\{{}\begin{matrix}x-1< =0\\x-5< =0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x< =1\\x< =5\end{matrix}\right.\)
=>x<=1
\(y=\sqrt{x^2-6x+5}\)
=>\(y'=\dfrac{\left(x^2-6x+5\right)'}{2\sqrt{x^2-6x+5}}\)
=>\(y'=\dfrac{2x-6}{2\sqrt{x^2-6x+5}}\)
Đặt y'>0
=>\(\dfrac{2x-6}{2\sqrt{x^2-6x+5}}>0\)
=>2x-6>0
=>x>3
kết hợp ĐKXĐ, ta được: x>5
Đặt y'<0
=>\(\dfrac{2x-6}{2\sqrt{x^2-6x+5}}< 0\)
=>2x-6<0
=>x<3
Kết hợp ĐKXĐ, ta được: x<1
Vậy: Hàm số nghịch biến trên (-\(\infty\);1) và đồng biến trên (5;+\(\infty\))

Do \(\left( { - 2\pi ; - \pi } \right) = \left( { - 2\pi ;\pi - 2\pi } \right)\) nên hàm số \(y = \cos x\) nghịch biến trên khoảng \(\left( { - 2\pi ; - \pi } \right)\)

Đáp án A
Ta có y = sin x - cos x = 2 sin x - π 4
Từ đây ta có thể loại đáp án C, do tập giá trị của hàm số là - 2 ; 2
Hàm số đã cho tuần hoàn với chu kỳ 2π do vậy ta xét sự biến thiên của hàm số trên đoạn (-π/4; 7π/4)
Ta có:
* Hàm số đồng biến trên khoảng (-π/4; 3π/4)
* Hàm số nghịch biến trên khoảng (3π/4; 7π/4)