K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2021
Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1
16 tháng 11 2021
Vì hàm số này đồng biến khi x>0 nên nếu x trong khoảng (0;1) thì hàm số đồng biến
22 tháng 7 2021
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
TA
22 tháng 7 2021
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
CM
11 tháng 8 2017
a) Sau khi tính giá trị của mỗi giá trị theo các giá trị của x đã cho ta được bảng sau:
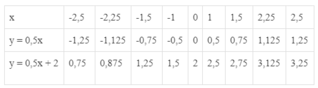
b) Nhận xét: Cùng một giá trị của biến x, giá trị của hàm số y = 0,5x + 2 luôn luôn lớn hơn giá trị tương ứng của hàm số y = 0,5x là 2 đơn vị.
NT
2
13 tháng 4 2017
vì căn 5 -2>0 => hàm số nghịch biến khi x<0, đồng biến khi x>0
15 tháng 4 2017
vì căn5 - 2 >0 nên hàm số đồng biến khi x>0, nghịch biến khi x<0
CM
24 tháng 3 2017
Hàm số y = f(x) = -1,5 x 2 có hệ số a = -1,5 < 0 nên hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
H
0
CM
2 tháng 3 2019
a) Ta có:
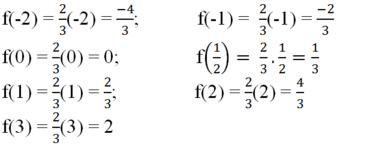
b) Ta có:
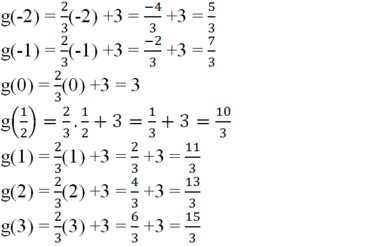
c) Từ kết quả câu a, b ta được bảng sau:
Nhận xét:
- Hai hàm số
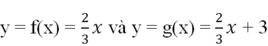
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
TT
1