Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

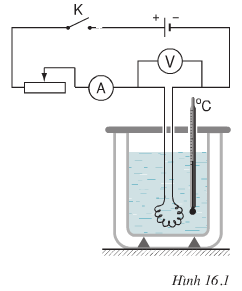
C1: Hãy tính điện năng A của dòng điện chạy qua dây điện trở trong thời gian trên.
Trả lời:
+ Điện năng A = I2Rt = (2,4)2.5.300 = 8640 J.
C2: Hãy tính nhiệt lượng Q mà nước và bình nhôm nhận được trong thời gian đó.
Trả lời:
+ Nhiệt lượng Q mà nước và bình nhôm nhận được: Q = Q1 + Q2 ; trong đó
Nhiệt lượng nước nhận được Q1 = c1m1 ∆to = 4200.0,2.9,5 = 7980 J.
Nhiệt lượng bình nhôm nhận được Q2 = c2m2 ∆to = 880.0,078.9,5 = 652 J.
Vậy Q = 7980 + 652 = 8632 J.
C3: Hãy so sánh A với Q và nêu nhận xét, lưu ý rằng có một phần nhỏ nhiệt lượng truyền ra môi trường xung quanh.
Trả lời:
+ So sánh: ta thấy A lớn hơn Q một chú. Điện năng tiêu thụ đã có một ít biến thành nhiệt lượng được truyền ra môi trường xung quanh.

a.P=2Vqcdqc−dnn−1b.dqc=89000N/m3a.P=2Vqcdqc−dnn−1b.dqc=89000N/m3
Giải thích các bước giải:
a.
F=Pqc−FA=Vqcdqc−Vqcdn=Vqc(dqc−dn)MAB=MqcP.12(OA−OB)=OB.F=OB.Vqc(dqc−dn)p=2.OB.Vqcdqc−dnnOB−OB=2Vqcdqc−dnn−1b.0,79.10=2.50.10−6dqc−100002−1dqc=89000N/m3

Nhiệt độ của nước đá đang tan là 00C, vì sau khi có cân bằng nhiệt hỗn hợp bao gồm cả nước và nước đá nên nhiệt độ của nó cũng là 00C.
Nhiệt lượng mà nước (350C) đã tỏa ra:
Qtỏa = mc (t1 – t0) = 1,5.4200.30 = 189 000 J
Gọi x là khối lượng nước đá đã bị nóng chảy. Nhiệt lượng mà nước đá thu vào để nóng chảy là:
Qthu = \(x.\lambda\) = 340000.x
Áp dụng phương trình cân bằng nhiệt:
Qtỏa = Qthu => 340 000 x = 189 000: 340 000 = 0,55 kg
Vậy khối lượng nước đá ban đầu là: 0,45 + 0,55 = 1,0 kg
Nhiệt độ nước đá đang tan là 0 độ c, vì sau khi có cân bằng nhiệt hỗn hợp bao gồm cả nước và nước đá nên nhiệt độ của nó cũng là 0 độ c
Nhiệt lượng mà nước ở 30 độ c đã toả ra:
Q1 = m.c. ∆t = 1,5.4200.30 = 189000J
Gọi x (kg) là khối lượng nước đá bị nóng chảy
Nhiệt lượng mà nước đá thu vào để nóng chảy là
Q2 = λ .x = x.3,4.105 J
Áp dụng phương trình cân bằng nhiệt lượng:
Q1=Q2<=> 189000=x.3,4.105 => x=0,55kg
Vậy khối lượng nước đá ban đầu là: 0,45+0,55=1kg

a/ Đổi 0,1mm2 = 1. 10-7 m2 . Áp dụng công thức tính điện trở \(R=\rho\frac{l}{S}\) ; thay số và tính \(\Rightarrow\) RAB = 6W
b/ Khi \(AC=\frac{BC}{2}\) \(\Rightarrow\) RAC = \(\frac{1}{3}\).RAB Þ RAC = 2W và có RCB = RAB - RAC = 4W
Xét mạch cầu MN ta có \(\frac{R_1}{R_{AC}}=\frac{R_2}{R_{CB}}=\frac{3}{2}\) nên mạch cầu là cân bằng. Vậy IA = 0
c/ Đặt RAC = x ( ĐK : \(0\le x\le6\Omega\) ) ta có RCB = ( 6 - x )
* Điện trở mạch ngoài gồm ( R1 // RAC ) nối tiếp ( R2 // RCB ) là \(R=\frac{3.x}{3+x}+\frac{6.\left(6-x\right)}{6+\left(6-x\right)}=\)= ?
* Cường độ dòng điện trong mạch chính : \(I=\frac{U}{R}\) ?
* Áp dụng công thức tính HĐT của mạch // có : UAD = RAD . I = \(\frac{3.x}{3+x}.I=\) ?
Và UDB = RDB . I = \(\frac{6.\left(6-x\right)}{12-x}I\) = ?
* Ta có cường độ dòng điện qua R1 ; R2 lần lượt là : I1 = \(\frac{U_{AD}}{R_1}\) = ? và I2 = \(\frac{U_{DB}}{R_2}\) = ?
+ Nếu cực dương của ampe kế gắn vào D thì : I1 = Ia + I2 Þ Ia = I1 - I2 = ? (1)
Thay Ia = 1/3A vào (1) Þ Phương trình bậc 2 theo x, giải PT này được x = 3W ( loại giá trị -18)
+ Nếu cực dương của ampe kế gắn vào C thì : Ia = I2 - I1 = ? (2)
Thay Ia = 1/3A vào (2) Þ Phương trình bậc 2 khác theo x, giải PT này được x = 1,2W ( loại 25,8 vì > 6 )
* Để định vị trí điểm C ta lập tỉ số \(\frac{AC}{CB}=\frac{R_{AC}}{R_{CB}}\) = ? \(\Rightarrow\) AC = 0,3m
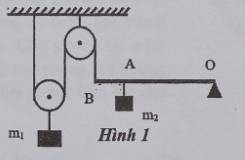


AD đk cân bằng momen ta có
`P_1/2 * OB = OA * P_2`
`<=> m_1/2 * OB = (OB - AB) * m_2`
`<=> 5/2 *OB = (OB -20) * 3`
`=> OB = 120(cm)`