
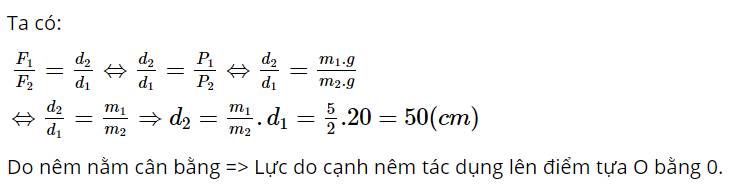
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

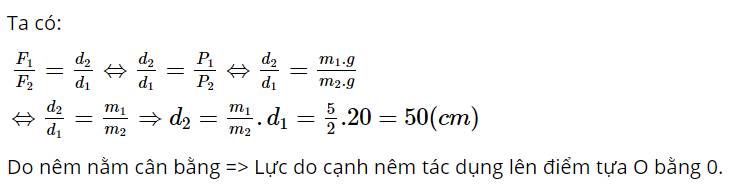

Ta có:
\(\begin{array}{l}\frac{{{F_1}}}{{{F_2}}} = \frac{{{d_2}}}{{{d_1}}} \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{{{P_1}}}{{{P_2}}} \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{{{m_1}.g}}{{{m_2}.g}}\\ \Leftrightarrow \frac{{{d_2}}}{{{d_1}}} = \frac{{{m_1}}}{{{m_2}}} \Rightarrow {d_2} = \frac{{{m_1}}}{{{m_2}}}.{d_1} = \frac{5}{2}.20 = 50(cm)\end{array}\)
Do nêm nằm cân bằng => Lực do cạnh nêm tác dụng lên điểm tựa O bằng 0.

Chọn D.
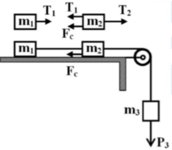
Chọn chiều dương là chiều chuyển động:
Xét hệ (m1 + m2 + m3) thì hai ngoại lực P3 và Fc làm cho hệ chuyển động với cùng một gia tốc có độ lớn:
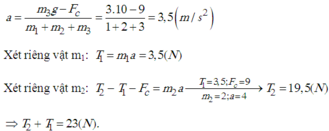

Hệ hai vật m 1 và m 2 chuyển động trong trọng trường, chỉ chịu tác dụng của trọng lực, nên cơ năng của hệ vật bảo toàn.
Vật m 1 , có trọng lượng P 1 = m 1 g ≈ 20 N và vật m2 có trọng lượng P 2 = m 2 g ≈ 1.10 = 10 N. Vì sợi dây nối hai vật này không dãn và P 1 > P 2 , nên vật m 1 chuyển động, thẳng đứng đi xuống và vật m 2 bị kéo trượt lên phía đỉnh mặt nghiêng với cùng đoạn đường đi và vận tốc. Như vậy, khi vật m 1 đi xuống một đoạn h thì thế năng của nó giảm một lượng W t 1 = m 1 gh, đồng thời vật m 2 cũng trượt lên phía đỉnh mặt nghiêng một đoạn h nên độ cao của nó tăng thêm một lượng hsinα và thế năng cũng tăng một lượng W t 2 = m 2 gh.
Theo định luật bảo toàn cơ năng, độ tăng động năng của hệ vật chuyển động trong trọng trường bằng độ giảm thế năng của hệ vật đó, tức là :
∆ W đ = - ∆ W t
⇒ 1/2( m 1 + m 2 ) v 2 = m 1 gh - m 2 gh.sin α
Suy ra W đ = 1/2( m 1 + m 2 ) v 2 = gh( m 1 - m 2 sin 30 ° )
Thay số, ta tìm được động năng của hệ vật khi vật m 1 đi xuống phía dưới một đoạn h = 50 cm :
W đ = 10.50. 10 - 2 .(2 - 1.0,5) = 7,5 J

Đáp án A
Áp dụng định luật II Niu - tơn ta có
a = F − μ 1 m 1 g − μ 2 m 2 g − μ 3 m 3 g m 1 + m 2 + m 3 = 35 − 0 , 3.5.10 − 0 , 2.5.10 − 0 , 1.5.10 5 + 5 + 5 = 1 3 m / s 2