Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

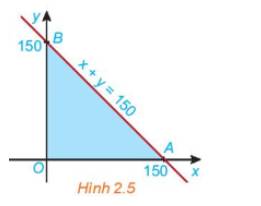
a) Thay tọa độ điểm O, A, B vào F(x;y) ta được:
F(0;0)=2.0+3.0=0
F(150;0)=2.150+3.0=300
F(0;150)=2.0+3.150=450.
b) Lấy một điểm bất kì trong miền tam giác OAB.
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x \ge 0\).
Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(y \ge 0\).
Vậy \(x \ge 0\) và \(y \ge 0\).
=> \(F\left( {x;y} \right) = 2x + 3y \ge 2.0 + 3.0 = 0\)
Vậy giá trị nhỏ nhất của F(x;y) trên miền OAB là 0.
c) Vì miền OAB là miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\) nên mọi điểm (x;y) thuộc miền OAB thỏa mãn \(x + y \le 150\)
Như vậy với mỗi điểm trong miền tam giác OAB thì đều có tổng \(x + y \le 150\)
Quan sát miền OAB ta thấy điểm B(0;150) là điểm có tung độ lớn nhất nên mọi điểm (x;y) thuộc miền OAB đều có \(y \le 150\).
Vậy ta có: \(F\left( {x;y} \right) = 2x + 3y\)\( = 2.\left( {x + y} \right) + y\)\( \le 2.150 + 150 = 450\)
Dấu “=” xảy ra khi x+y=150 và y=150. Hay x=0, y=150.
Giá trị lớn nhất trên miền OAB là 450 tại điểm B.


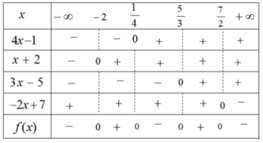
Nhị thức –3x – 3 có nghiệm là –1; nhị thức x + 2 có nghiệm là –2 ; nhị thức x + 3 có nghiệm là –3.
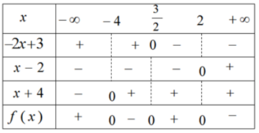
Ta có bảng xét dấu :

Kết luận :
+ f(x) < 0 khi –3 < x < –2 hoặc x > –1
+ f(x) > 0 khi x < –3 hoặc –2 < x < –1.
+ f(x) = 0 khi x = –3 hoặc x = –2 hoặc x = –1.
\(f\left(x;y\right)=3x^2+y^2-2x-xy+y+3\)
\(=\left(x^2-xy+\dfrac{y^2}{4}\right)+\dfrac{1}{2}\left(4x^2-4x+1\right)+\dfrac{1}{3}\left(\dfrac{9}{4}y^2+3y+1\right)+\dfrac{13}{6}\)
\(=\left(x-\dfrac{y}{2}\right)^2+\dfrac{1}{2}\left(2x-1\right)^2+\dfrac{1}{3}\left(\dfrac{3y}{4}+1\right)^2+\dfrac{13}{6}>0;\forall x;y\)