Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đỉnh của parabol là \(\frac{-\Delta}{4a}\) ta có
\(\left\{{}\begin{matrix}\frac{-\Delta}{4a}=-25\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\16a-4b+c=0\\36a+6b+c=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b^2-4ac=100a\\24a+c=0\\2a+b=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a^2-4ac=100a\\24a+c=0\\b=-2a\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-c=25\\24a+c=0\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=-24\end{matrix}\right.\)
\(\Rightarrow y=x^2-2x-24\)

+ Giao điểm của parabol với trục tung:
Tại x = 0 thì y = a.02 + b.0 + c = c.
Vậy giao điểm của parabol với trục tung là A(0 ; c).
+ Giao điểm của parabol với trục hoành :
Tại y = 0 thì ax2 + bx + c = 0 (*).
Để parabol cắt trục hoành tại hai điểm phân biệt thì phương trình (*) phải có 2 nghiệm phân biệt ⇔ Δ = b2 – 4ac > 0.
Khi Δ > 0 thì phương trình (*) có hai nghiệm là
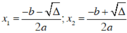
Tọa độ hai giao điểm là
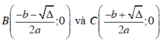

Parabol đi qua điểm M suy ra 6 = 25a – 5b + c (1)
Parabol cắt Oy tại điểm có tung độ bằng -2 nên -2 = a.0 + b.0 + c hay c = -2
Vậy 25a – 5b = 8
Chọn B.

Vì parabol cắt trục hoành tại hai điểm nên phương trình a x 2 + b x + c = 0 có 2 nghiệm hay Δ = b 2 − 4 a c > 0
Đỉnh của parabol là I − b 2 a ; − Δ 4 a . Điểm này nằm phía trên trục hoành nên tung độ điểm này lớn hơn 0, tức là − Δ 4 a > 0 . Mà Δ > 0 ⇒ a < 0
Chọn B.

a) Thay x=1 và y=-2 vào (P), ta được:
\(a\cdot1^2-4\cdot1+c=-2\)
\(\Leftrightarrow a-4+c=-2\)
hay a+c=-2+4=2
Thay x=2 và y=3 vào (P), ta được:
\(a\cdot2^2-4\cdot2+c=3\)
\(\Leftrightarrow4a-8+c=3\)
hay 4a+c=11
Ta có: \(\left\{{}\begin{matrix}a+c=2\\4a+c=11\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3a=-9\\a+c=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\c=2-a=2-3=-1\end{matrix}\right.\)
Vậy: (P): \(y=3x^2-4x-1\)

Lời giải:
$(P)$ cắt trục tung tại điểm có tung độ $-1$ tức $(P)$ đi qua $(0; -1)$
$\Rightarrow -1=a.0^2-2.0+c$
$\Rightarrow c=-1$
Để $P$ có min $=\frac{-4}{3}$ thì:
\(\left\{\begin{matrix}
a>0\\
\frac{4ac-b^2}{4a}=\frac{-4a-(-2)^2}{4a}=\frac{-4a-4}{4a}=\frac{-(a+1)}{a}=\frac{-4}{3}\end{matrix}\right.\)
\(\Leftrightarrow a=3\)
Vậy parabol là $y=3x^2-2x-1$
công thức này là công thức nào vậy ạ :\(\dfrac{4ac-b^2}{4a}\)

+ Parabol y = ax2 + bx + 2 đi qua điểm B(–1 ; 6)
⇒ 6 = a.( –1)2 + b.( –1) + 2 ⇒ a = b + 4 (1)
+ Parabol y = ax2 + bx + 2 có tung độ của đỉnh là –1/4
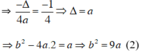
Thay (1) vào (2) ta được: b2 = 9.(b + 4) ⇔ b2 – 9b – 36 = 0.
Phương trình có hai nghiệm b = 12 hoặc b = –3.
Với b = 12 thì a = 16.
Với b = –3 thì a = 1.
Vậy có hai parabol thỏa mãn là y = 16x2 + 12b + 2 và y = x2 – 3x + 2.

(P) : y = ax2 + bx + c
Parabol có đỉnh I(1 ; 4) ⇒ –b/2a = 1 ⇒ b = –2a ⇒ 2a + b = 0.
Parabol đi qua I(1; 4) ⇒ 4 = a.12 + b . 1 + c ⇒ a + b + c = 4.
Paraol đi qua D(3; 0) ⇒ 0 = a.32 + b.3 + c ⇒ 9a + 3b + c = 0.
Giải hệ phương trình 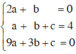
ta được : a = –1 ; b = 2 ; c = 3.
Vậy a = –1 ; b = 2 ; c = 3.

Sửa đề: cắt trục tung tại điểm có tung độ bằng -3
Thay x=0 và y=-3 vào (P), ta được:
\(a\cdot0^2+b\cdot0+c=-3\)
=>0+0+c=-3
=>c=-3
vậy: (P): \(y=ax^2+bx-3\)
Tọa độ đỉnh là I(-1;-4) nên ta có:
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{b^2-4\cdot a\cdot\left(-3\right)}{4a}=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\dfrac{b^2+12a}{4a}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\left(2a\right)^2+12a=16a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\4a^2-4a=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\4a\left(a-1\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=2a\\\left[{}\begin{matrix}a=0\left(loại\right)\\a-1=0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)