Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

bn ơi chắc gì đã là 1441 có khi là 1551, 1661, 1771, 1881, 199 ko bài này mình làm rồi nhưng mình không nhớ cách giải

. Tuổi của Toán học và Tuổi trẻ
năm 1994 là: 1994 -
abcd
=
2
3
x (a + b + c + d) (*)
Vì a + b + c + d ≤ 9 + 9 + 9 + 9 = 36 nên :
2
3
x (a + b + c + d) ≤
2
3
x 36 = 54.
Từ (*) ta thấy 1994 -
abcd
≤ 54 nên 1940 ≤
abcd
≤ 1994. Suy ra
ab
= 19 và 40 ≤
cd
≤
94. Thay
ab
= 19 vào (*) được : 94 -
cd
=
2
3
x ( 1 + 9 + c + d).
hay : 2 x (94 -
cd
) = 3 x (10 + c + d).
hay : 188 – 2 x (c x 10 + d) = 30 + c x 3 + d x 3.
hay : c x 23 + d x 5 = 158.
Vì d x 5 ≤ 45 nên suy ra 113 ≤ c x 23 ≤ 158.
Do đó 5 ≤ c ≤ 6.
- Nếu c = 5 thì d x 5 = 159 – 115 = 43, không tìm được số d nguyên.
- Nếu c = 6 thì d x 5 = 158 – 138 = 20 nên d = 4.
Thử lại : 1994 – 1964 =
2
3
x (1 + 9 + 6 + 4).
Vậy báo Toán học và Tuổi trẻ sinh năm 1964.

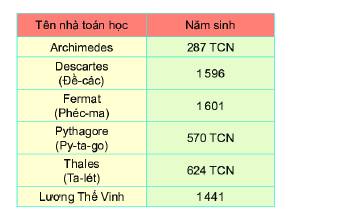
Archimedes: -287;
Đề-các: 1596;
Phéc-ma: 1601;
Py-ta-go: -570;
Ta-lét: -624;
Lương Thế Vinh: 1441.
Ta có \(1601 > 1596 > 1441 > \)\( - 287 > - 570 > - 624\) nên ta có năm sinh của các nhà toán học được sắp xếp theo thứ tự giảm dần là: 1601;1596;1441; 287 TCN; 570 TCN; 624 TCN.
Bài giải: Gọi năm sinh của hai ông là abba (a ≠ 0, a < 3, b <10).
Ta có: a + b + b + a = 10 hay (a + b) x 2 = 10. Do đó a + b = 5.
Vì a ≠ 0 và a < 3 nên a = 1 hoặc 2.
* Nếu a = 1 thì b = 5 - 1 = 4. Khi đó năm sinh của hai ông là 1441 (đúng).
* Nếu a = 2 thì b = 5 - 2 = 3. Khi đó năm sinh của hai ông là 2332 (loại).
Vậy hai ông Vũ Hữu và Lương Thế Vinh sinh năm 1441.
trong sach toan nang cao va phat trien chu dau
ai ma chang biet la 1441