Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

4.
(1) => y=2m-mx thay vào (2) ta được x+m(2m-mx)=m+1
<=> x-m2x=-2m2+m+1
<=> x(1-m)(1+m)=-(m-1)(1+2m)
với m=-1 thì pt vô nghiệm
với m=1 thì pt vô số nghiệm => có nghiệm nguyên => chọn
với m\(\ne\pm\) 1 thì x=\(\frac{-2m-1}{m+1}\)=\(-2+\frac{1}{m+1}\)
=> y=2m-mx=xm-m(-2+\(\frac{1}{m+1}\)) =2m+2m-\(\frac{m}{m+1}\)=4m-1+\(\frac{1}{m+1}\)
để x y nguyên thì \(\frac{1}{m+1}\)nguyên ( do m nguyên)
=> m+1\(\in\)Ư(1)={1;-1}
=> m\(\in\){0;-2} mà m nguyên âm nên m=-2
vậy m=-2 thì ...
P/s hình như 1 2 3 sai đề

a) + Xét phương trình 2x + y = 4 (1) ⇔ y = -2x + 4
Vậy phương trình (1) có nghiệm tổng quát là (x ; -2x + 4) (x ∈ R).
+ Xét phương trình 3x + 2y = 5 (2) ⇔ 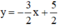
Vậy phương trình (2) có nghiệm tổng quát là : 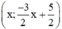 (x ∈ R).
(x ∈ R).
b) Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) : 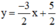
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒ 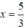
⇒ (d’) đi qua hai điểm (0; 2,5) và 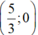
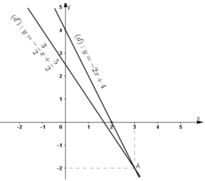
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2).

a) . Do đó phương trình có nghiệm dạng tổng quát như sau:
hoặc
b) Vẽ (d1): 2x + y = 4
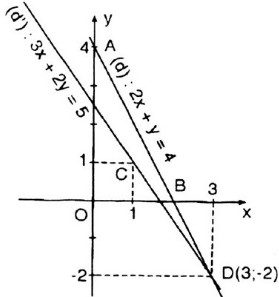
- Cho x = 0 => y = 4 được A(0; 4).
- Cho y = 0 => x = 2 được B(2; 0).
Vẽ (d2): 3x + 2y = 5
- Cho x = 0 => y =  được C(0;
được C(0;  ).
).
- Cho y = 0 => x =  được D(
được D( ; 0).
; 0).
Hai đường thẳng cắt nhau tại M(3; -2).
Thay x = 3, y = -2 vào từng phương trình ta được:
2 . 3 + (-2) = 4 và 3 . 3 + 2 . (-2) = 5 (thỏa mãn)
Vậy (x = 3; y = -2) là nghiệm chung của các phương trình đã cho.

Đường thẳng biểu diễn tập nghiệm của phương trình (1) là đường thẳng (d) : y = -2x + 4.
Chọn x = 0 ⇒ y = 4
Chọn y = 0 ⇒ x = 2.
⇒ (d) đi qua hai điểm (0; 4) và (2; 0).
Đường thẳng biểu diễn tập nghiệm của phương trình (2) là đường thẳng (d’) : 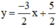
Chọn x = 0 ⇒ y = 2,5.
Chọn y = 0 ⇒ 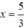
⇒ (d’) đi qua hai điểm (0; 2,5) và 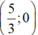
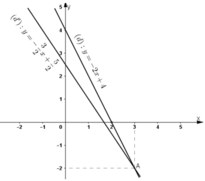
Hai đường thẳng cắt nhau tại A(3; -2).
Vậy (3; -2) là nghiệm chung của hai phương trình (1) và (2)

m thủa mãn hệ:
\(\left\{{}\begin{matrix}\Delta>0\left(1\right)\\P>0\left(2\right)\\s>0\left(3\right)\\x_2=3x_1\left(4\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\Delta'=1-\left(m-1\right)>0\Rightarrow m< 2\)
\(\left(2\right)\Leftrightarrow m-1>0\Rightarrow m>1\)
\(\left(3\right)\Leftrightarrow-\dfrac{-2}{1}>0\forall m\)
\(\left\{{}\begin{matrix}t_2=1-\sqrt{2-m}\\t_1=1+\sqrt{2-m}\end{matrix}\right.\) \(\left(4\right)\Leftrightarrow1+\sqrt{2-m}=9\left(1-\sqrt{2-m}\right)\Rightarrow10\sqrt{2-m}=8\Rightarrow m=\dfrac{34}{25}=1,36\)
Kết luận: \(m=1,36\)