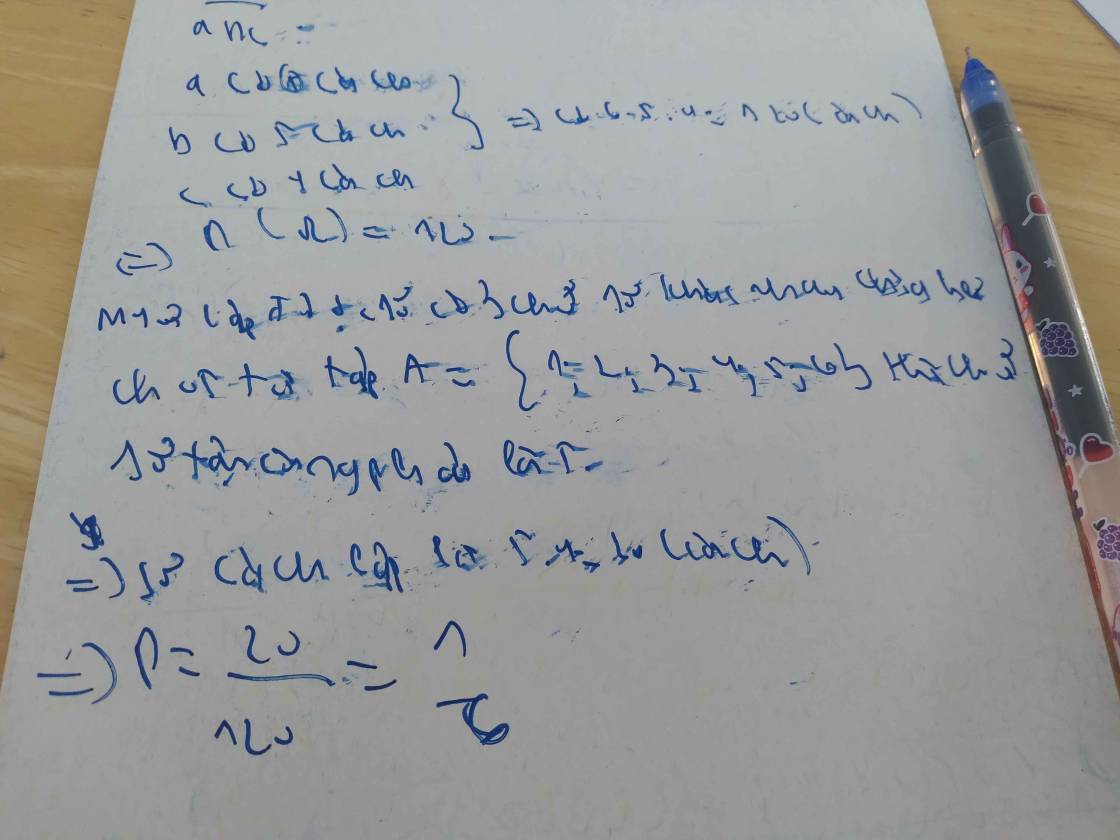Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Các số tự nhiên nhỏ hơn 1000 gồm các số có 1 chữ số, có 2 chữ số hoặc 3 chữ số.
+ Số có 1 chữ số chia hết cho 5 là: 0 và 5 => có 2 số.
+ Số có 2 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng chục có 9 cách chọn.
Hàng đơn vị là 5: chữ số hàng chục có 8 cách chọn (khác 0).
=> Có \(9 + 8 = 17\) (số)
+ Số có 3 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng trăm có 9 cách chọn, hàng chục có 8 cách chọn.
Hàng đơn vị là 5: chữ số hàng trăm có 8 cách chọn, hàng chục có 8 cách chọn.
=> Có 9.8+8.8 = 136 (số)
Vậy có tất cả \(2 + 17 + 136 = 155\) số thỏa mãn ycbt.

Các số lẻ có 2 chữ số giống nhau là:
11 , 33 , 55 , 77 , 99 .
Ta thấy mỗi số hơn kém nhau 22 đơn vị (33-11=22.......)
Số lượng số hạng là:
(99-11):22+1=5(số)
Tống của tất cả các số lẻ có 2 chữ số giống nhau là :
(99+11)x5:2=275
Tổng của tất cả các số lẻ có 2 chữ số giống nhau được gấp lên 9 lần là :
275x9=2475

Gọi số cần tìm là: abc
Các số có 2 chữ số được tạo thành là; ab; ba; ac; ca; bc; cb
Ta có: abc = ab + ba + ac + ca + bc + cb
a x 100 + b x 10 + c = 22 x a + 22 x b + 22 x c
78 x a = 12 x b + 21 x c
26 x a = 4 x b + 7 x c
4 x b + 7 x c lớn nhất là 4 x 9 + 7 x 9 = 99 nên a chỉ có thể bằng 1;2;
cần tìm số lớn nhất nên thử a = 3 => 4 x b + 7 x c = 52 là số chẵn
nên c phải chẵn => c = 4 và b = 6 thoả mãn
Đáp số: 264

a) Từ 4 chữ số 0, 1, 2, 3:
- Hàng trăm có 3 cách chọn.
- Hàng chục có 3 cách chọn.
- Hàng đơn vị có 2 cách chọn.
Vậy có tất cả 3.3.2 = 18 số tự nhiên khác nhau có 3 chữ số được lập từ 0, 1, 2, 3.
b) - Trường hợp 1: hàng đơn vị là số 0 như vậy hàng trăm có 3 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 3 = 6 số có thể lập được.
- Trường hợp 2: hàng đơn vị là số 2 như vậy hàng trăm có 2 cách chọn, hàng chục có 2 cách chọn.
Có tất cả 1. 2. 2 = 4 số có thể lập được.
Vậy có thể lập 6 + 4 = 10 số tự nhiên chẵn có ba chữ số khác nhau.

\(\overline{abcde}\)
TH1: e=0
e có 1 cách chọn
Chữ số 2 có 4 cách chọn
ba chỗ còn lại có 4*3*2=24 cách
=>Có 4*24=96 cách
TH2: e=5; a=2
a,e có 1 cach
b có 4 cách
c có 3 cách
dcó 2 cách
=>Có 4*3*2=24 cách
TH3: e=5; a<>2
e có 1 cách chọn
a có 3 cách chon
số 2 có 3 cách
hai số còn lại có 3*2=6 cách
=>Có 3*3*6=54 cách
=>CÓ 96+24+54=174 số

Ta có:
Từ 100\(\rightarrow\)190 có 20 chữ số 0
Từ 200\(\rightarrow\)290 có 20 chữ số 0
Từ 300\(\rightarrow\)390 có 20 chữ số 0
Từ 400\(\rightarrow\)490 có 20 chữ số 0
Số 500 có 2 chữ số 0
Do đó từ 1 đến 500 có số chữ số 0 là:
20x4+2=82(chữ số 0)
Xét chữ số 0 ở hàng đơn vị thì ta có dãy số:
100;110;120;...;500
Số chữ số 0 có từ hàng đơn vị là:
(500-100):10+1=41 (chữ số 0)
Xét chữ số 0 ở hàng chục từ số 100 tới 190
Ta có dãy số 100;101;102;...;109
Số chữ số 0 có từ hàng chục từ số 100 tới 190
(109-100):1+1=10 (chữ số 0)
Xét chữ số 0 ở hàng chục từ số 200 tới 290
Ta có dãy số 200;201;202;...;209
Số chữ số 0 có từ hàng chục từ số 100 tới 190
(209-200):1+1=10 (chữ số 0)
Tương tự em cũng giải như thế đến hết số 490(em tự làm)
Số chữ số 0 có từ hàng chục từ số 100 tới 490 là
10+10+10+10=40(chữ số 0)
Ta có số 500 có 1 chữ số 0 ở hàng chục
Số chữ số 0 có từ hàng chục từ số 100 tới 500 là
40+1=41(chữ số 0)
=>Số chữ số 0 có từ hàng chục,đơn vị từ số 100 tới 490 là
41+41=82(chữ số 0)

Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)

Đặt A=1+2+3+4+ ...+n=aaa
Ta có:1+2+3+4+ ...+n=aaa
(1+n).n:2=a.111
(1+n).n:2=a.3.37
(1+n).n=a.3.37.2
Vì a.3.37.2 chia hết cho 37
Nên (1+n).n cũng chia hết cho 37
Vậy n hoặc ( n + 1 ) phải chia hết cho 37
Mà a.3.2≤9.3.2
\(\Rightarrow\) a.3.2≤54
Nên n hoặc n+1 không thể là 74
Ta có 36.37 hoặc 37.38
Vì 38 không chia hết cho 6 nên n=36 và n+1=37
Vậy n = 36
Ta có 1+2+3+...+n=aaa(n,aEN)
<=> n*(n+1):2=a*111
<=> n*(n+1):2=a*3*37
<=>n*(n+1)=a*3*2*37
<=>n*(n+1)=6a*37(1)
Mà n và n+1 là 2 số tự nhiên liên tiếp
Nên 6a và 37 cũng là 2 số tự nhiên liên tiếp
=>6a=36 hoặc 6a=38
a=6 a=19/3(loại vì aEN)
Thay a=6 vào (1) ta có
n*(n+1)=36*37
=>n=36

Gọi B là tổng các chữ số của A. Ta có A = 123456...9899100
Lúc này ta cần tính B = 1 + 2 + ... + 8 + 9 + 1 +0 +1 + 1 + ... + 9 + 9 + 1 + 0 + 0
Ta sẽ tính sác xuất xuất hiện ( tức tần số suất hiện ) của các chữ số 0 ; 1 ; 2 ; ... ; 8 ; 9
Ta sẽ thấy 0 xuất hiện 11 lần ; 1 xuất hiện 21 lần còn các chữ số còn lại là 2 ; 3 ;... ;9 thì xuất hiện 20 lần
Vậy B = 0 x 1 + 1 x 21 + ( 2 + 3 + ... + 9 ) x 20 = 901 ko chia hết cho 9 nên ko thể chia hết cho 2007