Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi \(I\left(x;y\right)\) là tâm đường tròn \(\Rightarrow\overrightarrow{AI}=\left(x-1;y-3\right)\)
Do đường tròn tiếp xúc với \(d_1;d_2\) nên:
\(d\left(I;d_1\right)=d\left(I;d_2\right)\Rightarrow\dfrac{\left|5x+y-3\right|}{\sqrt{26}}=\dfrac{\left|2x-7y+1\right|}{\sqrt{53}}\)
Chà, đề đúng ko em nhỉ, thế này thì vẫn làm được nhưng rõ ràng nhìn 2 cái mẫu kia thì số liệu sẽ xấu 1 cách vô lý.
2.
Phương trình đường thẳng kia là gì nhỉ? \(2x+y=0\) à?

Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
d(I; d) = R
Ta có : R = d(I; d) = =
Phương trình đường tròn cần tìm là:
(x +1)2 + (y – 2)2 = =>( x +1)2 + (y – 2)2 =
<=> 5x2 + 5y2 +10x – 20y +21 = 0

Vì đường tròn cần tìm tiếp xúc với hai trục tọa độ nên các tọa độ xI ,yI của tâm I có thể là xI = yI hoặc xI = -yI
Đặt xI = a thì ta có hai trường hợp I(a ; a) hoặc I(-a ; a). Ta có hai khả năng:
Vì I nằm trên đường thẳng 4x – 2y – 8 = 0 nên với I(a ; a) ta có:
4a – 2a – 8 = 0 => a = 4
Đường tròn cần tìm có tâm I(4; 4) và bán kính R = 4 có phương trình:
(x – 4 )2 + (y – 4)2 = 42
x2 + y2 – 8x – 8y + 16 = 0
+ Trường hợp I(-a; a):
-4a – 2a – 8 = 0 => a =
Ta được đường tròn có phương trình:
+
=
Đường thẳng 4x-2y-8=0 chuyển về dạng tham số ta được
x=t
y=2t-4
Gọi I(t; 2t-4) thuộc đthẳng
Do đường tròn tiếp xúc với 2 trục tọa độ lên khoảng cách đến 2 trục là = nhau
-->t=2t-4
t=4
Vậy đường tròn có dạng : (x-4)^2 + (y-4)^2 = 16

Đề bài sai
Điểm \(M\left(-5;2\right)\) không thuộc \(\Delta\) nên (C) ko thể tiếp xúc với \(\Delta\) tại M
Cảm ơn thầy đã góp ý ạ, nếu đề bài đúng thì hướng làm ra sao vậy ạ?

Đáp án: B
Ta có:
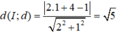
Vì đường tròn tiếp xúc với đường thẳng d nên R = d(I;d) = 5
Vậy phương trình đường tròn là: (x - 1 ) 2 + (y - 4 ) 2 = 5


Gọi pt đường tròn có dạng\(\left(C\right):\left(x-1\right)^2+\left(y+2\right)^2=R^2\)
Có \(R=d_{\left(A;d\right)}=\dfrac{\left|2.1-\left(-2\right)+6\right|}{\sqrt{2^2+1}}=\dfrac{10}{\sqrt{5}}\)
\(\Rightarrow R^2=20\)
\(\Rightarrow\left(C\right):\left(x-1\right)^2+\left(y+2\right)^2=20\)