Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì đường tròn cần tìm tiếp xúc với hai trục tọa độ nên các tọa độ xI ,yI của tâm I có thể là xI = yI hoặc xI = -yI
Đặt xI = a thì ta có hai trường hợp I(a ; a) hoặc I(-a ; a). Ta có hai khả năng:
Vì I nằm trên đường thẳng 4x – 2y – 8 = 0 nên với I(a ; a) ta có:
4a – 2a – 8 = 0 => a = 4
Đường tròn cần tìm có tâm I(4; 4) và bán kính R = 4 có phương trình:
(x – 4 )2 + (y – 4)2 = 42
x2 + y2 – 8x – 8y + 16 = 0
+ Trường hợp I(-a; a):
-4a – 2a – 8 = 0 => a =
Ta được đường tròn có phương trình:
+
=
Đường thẳng 4x-2y-8=0 chuyển về dạng tham số ta được
x=t
y=2t-4
Gọi I(t; 2t-4) thuộc đthẳng
Do đường tròn tiếp xúc với 2 trục tọa độ lên khoảng cách đến 2 trục là = nhau
-->t=2t-4
t=4
Vậy đường tròn có dạng : (x-4)^2 + (y-4)^2 = 16

Vì đường tròn cần tìm tiếp xúc với hai trục tọa độ nên các tọa độ xI ,yI của tâm I có thể là xI = yI hoặc xI = -yI
Đặt xI = a thì ta có hai trường hợp I(a ; a) hoặc I(-a ; a). Ta có hai khả năng:
Vì I nằm trên đường thẳng 4x – 2y – 8 = 0 nên với I(a ; a) ta có:
4a – 2a – 8 = 0 => a = 4
Đường tròn cần tìm có tâm I(4; 4) và bán kính R = 4 có phương trình:
(x - 4 )2 + (y – 4)2 = 42
x2 + y2 - 8x – 8y + 16 = 0
+ Trường hợp I(-a; a):
-4a - 2a - 8 = 0 => a =
Ta được đường tròn có phương trình:
+
=
o a b I x y
gọi pt đường trọng cần tìm là: \(\left(x-a\right)^2+\left(y-b\right)^2=R^2\left(C\right)\)
với I(a; b)
(C) tiếp xúc với 2 trục tọa độ \(\Rightarrow a=b=R\Rightarrow\left(C\right)\)co dang \(\left(x-a\right)^2+\left(y-a\right)^2=a^2\left(1\right)\)
lại có I(a;b) \(\in\) 4x-2y-8=0 \(\Rightarrow4a-2a-8=0\Rightarrow a=4\)
thay a = 4 vao (1) \(\Rightarrow\left(C\right)\left(x-4\right)^2+\left(y-4\right)^2=16\)

a) Ta tìm bán kính R2 = IM2 => R2 = IM = (2 + 2)2 + (-3 -32) = 52
Phương trình đường tròn (C): (x +2)2 + (y – 3)2 =52
b) Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
d(I; d) = R
Ta có : R = d(I; d) = \(=\)
Phương trình đường tròn cần tìm là:
(x +1)2 + (y – 2)2 = =>( x +1)2 + (y – 2)2 =
<=> 5x2 + 5y2 +10x – 20y +21 = 0
c) Tâm I là trung điểm của AB, có tọa độ :
x = \(\dfrac{1+7}{2}\) = 4; y = \(\dfrac{1+5}{2}\) = 3 => I(4; 3)
AB = \(2\sqrt{13}\) => R =\(\sqrt{13}\)
=> (x -4 )2 + (y – 3)2 =13

a) (C) có tâm I và đi qua M nên bán kính R = IM
Ta có: 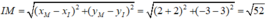
Vậy đường tròn (C) : (x + 2)2 + (y – 3)2 = 52.
b) (C) tiếp xúc với (Δ) : x – 2y + 7 = 0
⇒ d(I; Δ) = R
Mà 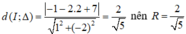
Vậy đường tròn (C) : 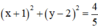
c) (C) có đường kính AB nên (C) có :
+ tâm I là trung điểm của AB
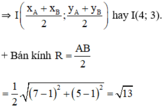
Vậy đường tròn (C) : (x – 4)2 + (y – 3)2 = 13.

Do tâm (C) thuộc \(\Delta\) nên có dạng: \(I\left(-2a-3;a\right)\)
\(d\left(I;d\right)=R\Leftrightarrow\dfrac{\left|-2a-3-a+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=\sqrt{2}\)
\(\Leftrightarrow\left|3a+2\right|=2\Rightarrow\left[{}\begin{matrix}a=0\\a=-\dfrac{4}{3}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(-3;0\right)\\I\left(-\dfrac{1}{3};-\dfrac{4}{3}\right)\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn: \(\left[{}\begin{matrix}\left(x+3\right)^2+y^2=2\\\left(x+\dfrac{1}{3}\right)^2+\left(y+\dfrac{4}{3}\right)^2=2\end{matrix}\right.\)

a) Phương trình đường tròn \(\left( C \right)\) là: \({\left( {x + 2} \right)^2} + {\left( {y - 5} \right)^2} = 49\).
b) Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( { - 2 - 1} \right)}^2} + {{\left( {2 - \left( { - 2} \right)} \right)}^2}} = 5\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 2} \right)^2} = 25\)
c) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( { - 2;1} \right)\)
Bán kính đường tròn là: \[R = IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( { - 3 - 1} \right)}^2}} = \sqrt {17} \]
Phương trình đường tròn là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 17\)
d) Bán kính đường tròn là: \(R = \frac{{\left| {1 + 2.3 + 3} \right|}}{{\sqrt {{1^2} + {2^2}} }} = 2\sqrt 5 \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 3} \right)^2} = 20\)


Đường tròn tiếp xúc với đường thẳng d nên khoảng cách từ tâm I tới đường thẳng d phải bằng bán kính đường tròn:
d(I; d) = R
Ta có : R = d(I; d) = =
= 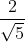
Phương trình đường tròn cần tìm là:
(x +1)2 + (y – 2)2 =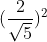 =>( x +1)2 + (y – 2)2 =
=>( x +1)2 + (y – 2)2 = 
<=> 5x2 + 5y2 +10x – 20y +21 = 0
5x2 + 5y2 +10x – 20y +6 mà