Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \({u_n} = 3n,\;\forall n \in {N^*}\).
b) Ta có: \({u_n} = 4n + 1,\forall n \in {N^*}\;\).

b, Số có 4 chữ số có dạng \(\overline{abcd}\).
a có 7 cách chọn.
b có 7 cách chọn.
c có 6 cách chọn.
d có 5 cách chọn.
\(\Rightarrow\) có \(7.7.6.5=1470\) số thỏa mãn.

gọi số cần tìm là abcdef( có gạch trên đầu b nhé)
với đk a#0 abcdef khác nhau
1; a có 8 cách chọn
b có 7 cách chọn
c có 6 cách chọn
d có 5 cách chọn
e có có 4 cách chọn
f có 3 cách chọn
=> có 20160 số tmycbt

Đáp án A
Chọn 10 tấm bất kì có C 30 10
trong 30 thẻ có 15 thẻ mang số chẵn
15 thẻ mang số lẻ và 3 số chia hết cho 10
Ta chọn 10 tấm thẻ lấy ra có 5 tấm thẻ mang số lẻ và 5 tấm thẻ mang số chẵn
trong đó chỉ có 1 tấm mang số chia hết cho 10 có
![]()
Do đó xác suất cần tìm là
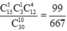
#include <bits/stdc++.h>
using namespace std;
int B[100],n,t;
{
cin>>n;
for (int i=1; i<=n; i++) cin>>B[i];
t=0;
for (int i=1; i<=n; i++)
if (B[i]%10==0) t+=B[i];
cout<<t<<endl;
int dem=0;
for (int i=1; i<=n; i++)
if ((i%2==0) && (A[i]%2!=0)) dem++;
cout<<dem<<endl;
for (int i=1; i<=n; i++)
if ((A[i]%2!=0) && (A[i]%3==0)) cout<<A[i];
}