Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
"Một số lẻ chữ số 1 và 1 số chẵn chữ số 2" nghĩa là sao nhỉ?
Bạn có thể ghi 1 cách chính xác tuyệt đối đề bài không?
Cách chọn số đầu tiên : 7 cách
Cách chọn số thứ 2: 7 cách
=> Không gian mẫu: \(n\left(\Omega\right)=7.7=49\)
a/ Gọi số chẵn là \(\overline{ab}\)
Xét b=0 => Có 1 cách chọn b và 7 cách chọn a
Xét b= 2;4;6=> có 3 cách chọn b và 6 cách chọn a
=> Có 1.7+3.6=25 (số chẵn)
=> \(n\left(A\right)=25\Rightarrow p\left(A\right)=\dfrac{25}{49}\)
b/ Gọi số chia hết cho 5 có dạng \(\overline{cd}\)
Xét d=0 => Có 1 cách chọn d và 7 cách chọn c
Xét d=5 => Có 1 cách chọn d và 6 cách chọn c
=> Có 1.7+ 1.6=13 (số chia hết cho 5)
\(\Rightarrow n\left(B\right)=13\Rightarrow p\left(B\right)=\dfrac{13}{49}\)
c/ Các số chia hết cho 9 có dạng \(\overline{ef}\)
\(e+f=9\Rightarrow\left(e;f\right)=\left(2;7\right);\left(3;6\right);\left(4;5\right)\)
\(\Rightarrow co:2!.3=6\left(so-chia-het-cho-9\right)\)
\(\Rightarrow n\left(C\right)=6\Rightarrow p\left(C\right)=\dfrac{6}{49}\)
Chọn C
Ta có 
Gọi số tự nhiên cần tìm có bốn chữ số là a b c d ¯
Vì a b c d ¯ chia hết cho 11 nên (a + c) - (b + d) ⋮ 11
=> (a + c) - (b + d) = 0 hoặc (a + c) - (b + d) = 11 hoặc (a + c) - (b + d) = -11 do
Theo đề bài ta cũng có a + b + c + d chia hết cho 11
Mà 
hoặc 
Vì 
nên (a + c) - (b + d) và a + b + c + d cùng tính chẵn, lẻ
(do các trường hợp còn lại không thỏa mãn) => (a,c) và (b,d) là một trong các cặp số:
- Chọn 2 cặp trong số 4 cặp trên ta có C 4 2 cách.
- Ứng với mỗi cách trên có 4 cách chọn a; 1 cách chọn c; 2 cách chọn b; 1 cách chọn d.
Vậy xác suất cần tìm là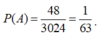 
.
Đáp án B.
Số phần tử của E là 
.
Từ 5 chữ số đã cho ta có 4 bộ gồm 3 chữ số có tổng chia hết cho 3 là 
. Mỗi bộ 3 chữ số này ta lập được 
số thuộc tập hợp E. Vậy trong tập hợp E có 
số chia hết cho 3.
Gọi A là biến cố “Số được chọn từ E chia hết cho 3” thì 
.
Vậy xác suất cần tính là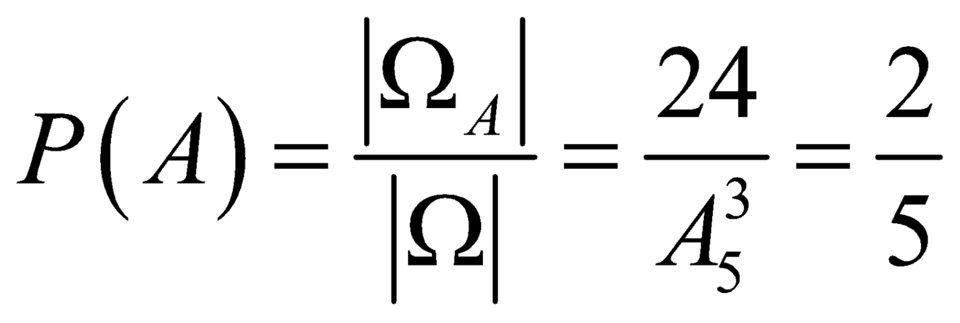 
.
Có 900 số tự nhiên có 3 chữ số \( \Rightarrow n\left( \Omega \right) = 900\)
Gọi \({A_1}\) là biến cố: “Số được chọn chia hết cho 2”, \({A_2}\) là biến cố “Số được chọn chia hết cho 7”.
Vậy \({A_1}{A_2}\) là biến cố “Số được chọn chia hết cho 14”, \(A = {A_1} \cup {A_2}\) là biến cố “Số được chọn chia hết cho 2 hoặc 7”.
Có 450 số có 3 chữ số chia hết cho 2 \( \Rightarrow n\left( {{A_1}} \right) = 450 \Rightarrow P\left( {{A_1}} \right) = \frac{{n\left( {{A_1}} \right)}}{{n\left( \Xi \right)}} = \frac{{450}}{{900}} = \frac{1}{2}\)
Có 128 số có 3 chữ số chia hết cho 7 \( \Rightarrow n\left( {{A_2}} \right) = 128 \Rightarrow P\left( {{A_2}} \right) = \frac{{n\left( {{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{128}}{{900}} = \frac{{32}}{{225}}\)
Có 64 số có 3 chữ số chia hết cho 14
\( \Rightarrow n\left( {{A_1}{A_2}} \right) = 64 \Rightarrow P\left( {{A_1}{A_2}} \right) = \frac{{n\left( {{A_1}{A_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{64}}{{900}} = \frac{{16}}{{225}}\)
\( \Rightarrow P\left( A \right) = P\left( {{A_1} \cup {A_2}} \right) = P\left( {{A_1}} \right) + P\left( {{A_2}} \right) - P\left( {{A_1}{A_2}} \right) = \frac{1}{2} + \frac{{32}}{{225}} - \frac{{16}}{{225}} = \frac{{257}}{{450}}\)
Gọi \({B_1}\) là biến cố: “Số được chọn có 3 chữ số chẵn”, \({B_2}\) là biến cố “Số được chọn có 1 chữ số chẵn và 2 chữ số lẻ”.
Vậy \(B = {B_1} \cup {B_2}\) là biến cố “Số được chọn có tổng các chữ số là số chẵn”.
Có \(4.5.5 = 100\) số có 3 chữ số chẵn \( \Rightarrow n\left( {{B_1}} \right) = 100 \Rightarrow P\left( {{B_1}} \right) = \frac{{n\left( {{B_1}} \right)}}{{n\left( \Omega \right)}} = \frac{{100}}{{900}} = \frac{1}{9}\)
Có \(4.5.5 = 100\) số có 3 chữ số có chữ số hàng trăm chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng chục chẵn, 2 chữ số còn lại lẻ.
Có \(5.5.5 = 125\) số có 3 chữ số có chữ số hàng đơn vị chẵn, 2 chữ số còn lại lẻ.
\( \Rightarrow n\left( {{B_2}} \right) = 100 + 125 + 125 = 350 \Rightarrow P\left( {{B_2}} \right) = \frac{{n\left( {{B_2}} \right)}}{{n\left( \Omega \right)}} = \frac{{350}}{{900}} = \frac{7}{{18}}\)
Vì \({B_1}\) và \({B_2}\) là hai biến cố xung khắc nên ta có:
\(P\left( B \right) = P\left( {{B_1} \cup {B_2}} \right) = P\left( {{B_1}} \right) + P\left( {{B_2}} \right) = \frac{1}{9} + \frac{7}{{18}} = \frac{1}{2}\)
Đáp án A.
Gọi số cần tìm có dạng a b c d vì chia hết cho 6
⇒ d = { 2 , 4 , 6 , 8 } a + b + c + d : 3
Khi đó, chọn d có 4 cách chọn, b và c đều có 9 cách chọn (từ 1 → 9).
+) Nếu a + b + c + d : 3 thì a = {3,6,9} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 1 thì a = {2,5,8} => có 3 cách chọn a.
+) Nếu a + b + c + d : 3 dư 2 thì a = {1,4,7} => có 3 cách chọn a.
Suy ra a chỉ có 3 cách chọn => có 4.9.9.3 = 972 số chia hết cho 6.
Vậy xác suất cần tính là P = 972 9 4 = 4 27 .