
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

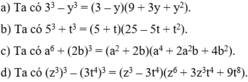

a/ \(\left(z^3\right)^3-\left(3t^4\right)^3=\left(z^3-3t^4\right)\left(z^6+3z^3t^4+9t^8\right)\)
b/ \(\left(\frac{x}{2}\right)^3-\left(3y^2\right)^3=\left(\frac{x}{2}-3y^2\right)\left(\frac{x^2}{4}+\frac{3}{2}xy^2+9y^4\right)\)

a) 25x² - 16
= (5x)² - 4²
= (5x - 4)(5x + 4)
b) 16a² - 9b²
= (4a)² - (3b)²
= (4a - 3b)(4a + 3b)
c) 8x³ + 1
= (2x)³ + 1³
= (2x + 1)(4x² - 2x + 1)
d) 125x³ + 27y³
= (5x)³ + (3y)³
= (5x + 3y)(25x² - 15xy + 9y²)
e) 8x³ - 125
= (2x)³ - 5³
= (2x - 5)(4x² + 10x + 25)
g) 27x³ - y³
= (3x)³ - y³
= (3x - y)(9x² + 3xy + y²)
a) \(25x^2-16=\left(5x-4\right)\left(5x+4\right)\)
b) \(16a^2-9b^2=\left(4a-3b\right)\left(4a+3b\right)\)
c) \(8x^3+1=\left(2x+1\right)\left(4x^2-2x+1\right)\)
d) \(125x^3+27y^3=\left(5x+3y\right)\left(25x^2-15xy+9y^2\right)\)
e) \(8x^3-125=\left(2x-5\right)\left(4x^2-10x+25\right)\)
g) \(27x^3-y^3=\left(3x-y\right)\left(9x^2+3xy+y^2\right)\)

a) x 2 + y 2 3 . b) ( m + 3 n ) 3 .
c) ( 2 u + 4 v ) 3 . d) ( z – t + 5 ) 3 .

\(27-x^3\)
\(=3^3-x^3\)
\(=\left(3-x\right)\left(9+3x+x^2\right)\)
\(8x^3+0,001\)
\(=\left(2x\right)^3+\left(\dfrac{1}{10}\right)^3\)
\(=\left(2x+\dfrac{1}{10}\right)\left(4x^2-2x\dfrac{1}{10}+\left(\dfrac{1}{10}\right)^2\right)\)
\(=2\left(x+\dfrac{1}{5}\right)\left(4x^2-\dfrac{1}{5}x+\dfrac{1}{100}\right)\)
\(\dfrac{x^3}{125}-\dfrac{y^3}{27}\)
\(=\left(\dfrac{x}{5}\right)^3-\left(\dfrac{y}{3}\right)^3\)
\(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left[\left(\dfrac{x}{5}\right)^2+\dfrac{x}{5}.\dfrac{y}{3}+\left(\dfrac{y}{3}\right)^2\right]\)
\(=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left(\dfrac{x^2}{25}+\dfrac{xy}{15}+\dfrac{y^2}{9}\right)\)
b )
Dấu = thứ 3 :
Sửa lại : \(2\left(x+\dfrac{1}{20}\right)\)

\(a,=8\left(x^3-125\right)=8\left(x-5\right)\left(x^2+5x+25\right)\\ b,=\left(0,1+4x\right)\left(0,01-0,4x+16x^2\right)\\ c,=\left(x+\dfrac{1}{5}y\right)\left(x^2-\dfrac{1}{5}xy+\dfrac{1}{25}y^2\right)\\ d,=\left(3x-\dfrac{1}{2}y\right)\left(9x^2+\dfrac{3}{2}xy+\dfrac{1}{4}y^2\right)\\ e,=\left(x-1+3\right)\left[\left(x-1\right)^2-3\left(x-1\right)+9\right]\\ =\left(x+2\right)\left(x^2-2x+1-3x+3+9\right)\\ =\left(x+2\right)\left(x^2-5x+13\right)\\ f,=\left(\dfrac{x^2}{2}-y^2\right)\left(\dfrac{x^4}{4}+\dfrac{x^2y^2}{2}+y^4\right)\)

\(a,27-x^3\)
\(=3^3-x^3\)
\(=\left(3-x\right)\left(9+3x+x^2\right)\)
Các câu còn lại lm tương tự nhé.
hok tốt!
a) \(27-x^3=\left(3-x\right)\left(9+3x+x^2\right)\)
b) \(8x^3+0,001=\left(2x+0,1\right)\left(4x^2-0,2x+0,01\right)\)
c) \(\frac{x^3}{125}-\frac{y^3}{27}=\left(\frac{x}{5}-\frac{y}{3}\right)\left(\frac{x^2}{25}+\frac{xy}{15}+\frac{y^2}{9}\right)\)
p/s: chúc bạn học tốt

\(a,=\left(3+x\right)\left(9-3x+x^2\right)\\ b,=\left(4x+0,1\right)\left(16x^2-0,4x+0,01\right)\\ c,=\left(2-3x\right)\left(4+6x+9x^2\right)\\ d,=\left(\dfrac{x}{5}-\dfrac{y}{3}\right)\left(\dfrac{x^2}{25}+\dfrac{xy}{15}+\dfrac{y^2}{9}\right)\)

a) \(8y^3+1\)
\(=\left(2y\right)^3+1^3\)
\(=\left(2y+1\right)\left(4y^2-2y+1\right)\)
b) \(y^3-8\)
\(=y^3-2^3\)
\(=\left(y-2\right)\left(y^2+2y+4\right)\)
`8y^3 + 1 = (2y+1)(4y^2 - 2y + 1)`
`y^3 -8 =(y-2)(y^2+2y+4)`

\(a)27{{\rm{x}}^3} + 1 = {\left( {3{\rm{x}}} \right)^3} + 1 = \left( {3{\rm{x}} + 1} \right).\left[ {{{\left( {3{\rm{x}}} \right)}^2} - 3{\rm{x}}.1 + {1^2}} \right] = \left( {3{\rm{x}} + 1} \right)\left( {9{{\rm{x}}^2} - 3{\rm{x}} + 1} \right)\)
\(b)64 - 8{y^3} = {4^3} - {\left( {2y} \right)^3} = \left( {4 - 2y} \right)\left[ {{4^2} + 4.2y + {{\left( {2y} \right)}^2}} \right] = \left( {4 - 2y} \right)\left( {16 + 8y + 4{y^2}} \right)\)

a: \(x^4+4=x^4+4x^2+4-4x^2=\left(x^2+2-2x\right)\left(x^2+2+2x\right)\)
c: \(x^3-125=\left(x-5\right)\left(x^2+5x+25\right)\)
\(\dfrac{1}{8}x^3-64=\left(\dfrac{1}{2}x-4\right)\left(\dfrac{1}{4}x^2+2x+16\right)\)
d: \(=\left(2x+5y\right)^3\)