
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC

| GT | ΔABC vuông tại A, BD là phân giác. DE vuông góc BC tại E AB giao DE=F |
| KL | BD là trung trực của AE |

`\text {GT | Cho đoạn thẳng BC, I là trung điểm của BC. Trên trung trực của BC lấy A (A} \ne \text {I)}`
`\text {KL |} \Delta AIB = \Delta AIC}`

a: Xét ΔOAH vuông tại A và ΔOBH vuông tại B có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)
Do đó: ΔOAH=ΔOBH
Suy ra: OA=OB; AH=BH
b: Xét ΔBHE vuông tại B và ΔAHM vuông tại A có
HB=HA
\(\widehat{BHE}=\widehat{AHM}\)
Do đó: ΔBHE=ΔAHM
Suy ra: HE=HM
c: Ta có: OM=OE
nên O nằm trên đường trung trực của ME(1)
Ta có: HE=HM
nên H nằm trên đường trung trực của ME(2)
Từ (1) và (2) suy ra OH là đường trung trực của ME

Ta có:
\(\sqrt{3x+4}=\sqrt{5x+4}\)
=> 3x + 4 = 5x + 4
=> 3x - 5x = 4 - 4
=> -2x = 0
=> x = 0

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

a: Xét tứ giác EFBC có
A là trung điểm của EB
A là trung điểm của CF
Do đó: EFBC là hình bình hành
Suy ra: EF=BC

1. Xét tam giác ABD và tam giác AED có:
\(\text{+}\) AD chung.
\(\text{+}\) \(\widehat{BAD}=\widehat{EAD}\) (AD là phân giác).
\(\text{+}\) AB = AE (gt).
\(\Rightarrow\) Tam giác ABD = Tam giác AED (c - g - c).
2. a) Tam giác ABD = Tam giác AED (cmt).
\(\Rightarrow\) \(\widehat{ABD}=\widehat{AED}\) (2 góc tương ứng).
Mà \(\widehat{ABD}+\widehat{KBD}=\)\(180^o.\)
\(\widehat{AED}+\widehat{CED}=\)\(180^o.\)
\(\Rightarrow\) \(\widehat{KBD}=\widehat{CED} (đpcm).\)
b) Xét tam giác KBD và tam giác CED có:
\(\text{+}\) \(\widehat{KBD}=\widehat{CED} \) (cmt).
\(\text{+}\) BD = ED (Tam giác ABD = Tam giác AED).
\(\text{+}\) \(\widehat{BDK}=\widehat{EDC}\) (2 góc đối đỉnh).
\(\Rightarrow\) Tam giác KBD = Tam giác CED (g - c - g).
3. Ta có: KE = KD + DE; CB = CD + DB.
Mà KD = CD (Tam giác KBD = Tam giác CED).
DE = DB (Tam giác ABD = Tam giác AED).
\(\Rightarrow\) KE = CB.
Xét tam giác KBE và tam giác CEB có:
\(\text{+}\) KE = CB (cmt).
\(\text{+}\) BK = EC (Tam giác KBD = Tam giác CED).
\(\text{+}\) BE chung.
\(\Rightarrow\) Tam giác KBE = Tam giác CEB (c - c - c).
4. Ta có: DE \(\perp\) AC (gt). => Tam giác AED vuông tại E.
Mà tam giác ABD = tam giác AED (cmt).
\(\Rightarrow\) Tam giác ABD vuông tại B.
\(\Rightarrow\) \(\widehat{ABD}\) \(=90^o.\)
\(\Rightarrow\) Tam giác ABC vuông tại B.
Vậy để DE \(\perp\) AC thì tam giác ABC vuông tại B.
 vẽ GT,Kl và hình ạ
vẽ GT,Kl và hình ạ cho mik GT,KL với ạ,( ko cần giải ạ)
cho mik GT,KL với ạ,( ko cần giải ạ)




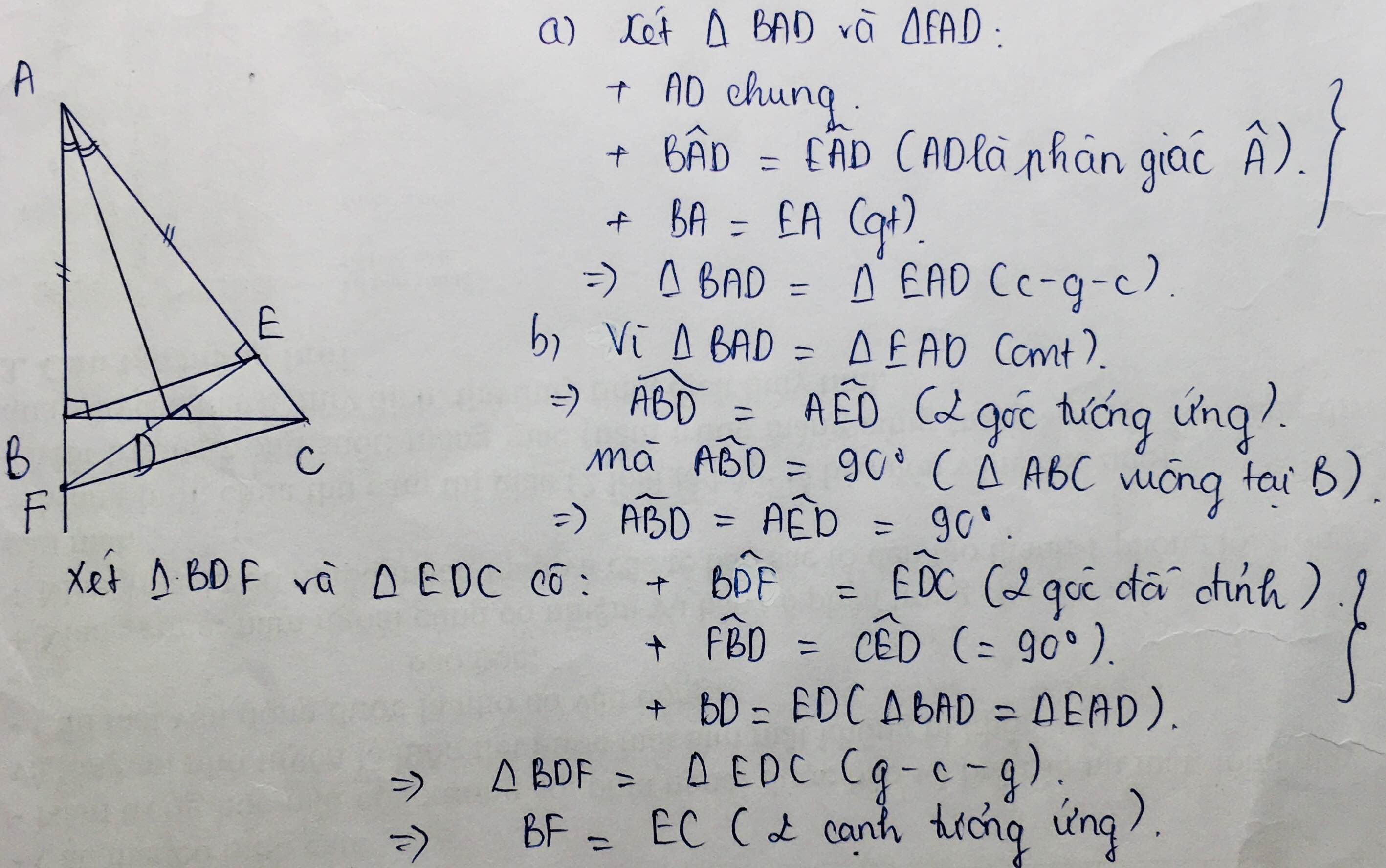



a: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
b: BA=BH
EA=EH
=>BE là trung trực của AH
c: AE=EH
EH<EC
=>AE<EC