Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D H m n
Gọi tỉ số diện tích tam giác ABD và diện tích tam giác ACD bằng \(\frac{m}{n}\)
Kẻ \(AH\perp BC\)
Ta có: \(S_{ABD}=\frac{1}{2}AH.BD\)và \(S_{ADC}=\frac{1}{2}AH.DC\)
\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mặt khác: AD là đường phân giác của tam giác ABC
\(\Rightarrow\frac{BD}{DC}=\frac{AB}{AC}=\frac{m}{n}\)
Gọi DM và DN lần lượt là đường cao của tam giác ADB và tam giác ACD
Xét tam giác ADB và tam giác ACD có :
góc BAD=góc DAC (gt)
AD chung
góc AMD = góc AND ( = 90 độ )
=> Tam giác ADB = tam giác ACD ( ch-gn)
=> DM=DN
TA có :
Stam giác ABD/Stam giác ADC
=(1/2.DM.AB)/(1/2.DN.AC)
=(1/2.DM.AB)/(1/2.DM.AC)=AB/AC=m/n (đpcm)
Như vầy cũng được mà trên mạng nó có mà sao bạn không chịu tìm nhỉ ???

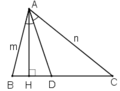
Kẻ AH là đường cao của tam giác ABC
Ta có:

Vậy tỉ số diện tích của tam giác ABD và tam giác ACD bằng m/n.

a/ Theo tính chất đường phân giác trong tam giác: Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn tỉ lệ với hai cạnh kề của hai đoạn ấy ta có
\(\frac{BD}{CD}=\frac{AB}{AC}=\frac{m}{n}\)
Hai tam giác ABD và tam giác ACD có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{BD}{CD}=\frac{m}{n}\)
b/ Ta có
\(\frac{S_{\Delta ABD}}{S_{\Delta ACD}}=\frac{m}{n}\Rightarrow\frac{S_{\Delta ABD}}{m}=\frac{S_{\Delta ACD}}{n}=\frac{S_{\Delta ABD}+S_{\Delta ACD}}{m+n}=\frac{S_{\Delta ABC}}{m+n}=\frac{s}{m+n}\)
\(\Rightarrow S_{\Delta ABD}=\frac{sm}{m+n}\)
Xét hai tam giác ABM và tam giác ABC có chung đường cao hạ từ A xuống BC nên
\(\frac{S_{\Delta ABM}}{S_{\Delta ABC}}=\frac{BD}{BC}=\frac{1}{2}\Rightarrow S_{\Delta ABM}=\frac{S_{\Delta ABC}}{2}=\frac{s}{2}\)
Mà \(S_{\Delta ADM}=S_{\Delta ABM}-S_{\Delta ABD}=\frac{s}{2}-\frac{sm}{m+n}\)

Kẻ AH ⊥ BC
Ta có:
SABD = 1212AH.BD
SADC = 1212AH.DC
=>SSBDSADCSSBDSADC = 12AH.BD12AH.DC12AH.BD12AH.DC = BDDCBDDC
Mặt khác: AD là đường phân giác của ∆ABC
=> BDDCBDDC= ABACABAC = mnmn.
Vậy SSBDSADCSSBDSADC = mn
kẻ AH là đường cao của tam giác ABD và cũng là đường cao của tam giác ACD.
\(\dfrac{SABD}{SACD}=\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC}=\dfrac{BD}{DC}\) (1)
TA CÓ:\(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{m}{n}\left(2\right)\)
Từ (1) và (2) =>\(\dfrac{SABD}{SADC}=\dfrac{m}{n}\)

1)
A B H D c m n
Kẻ AH là đường cao của ABC
Ta có :\(S_{ABCD}=\frac{1}{2}.AH.BD ; S_{ADC}=\frac{1}{2}.AH.CD\)
\(\Rightarrow\frac{S_{ABC}}{S_{ADC}}=\frac{\frac{1}{2}.AH.BD}{\frac{1}{2}.AH.CD}=\frac{BD}{CD}\left(1\right)\)
\(\Delta ABC\)có AD là tia phân giác
\(\Rightarrow\frac{BD}{CD}=\frac{AB}{AC}\left(2\right)\)
Từ (1)(2)
\(\Rightarrow\frac{S_{ABCD}}{S_{ACD}}=\frac{AB}{AC}=\frac{m}{n}\)
Vậy tỉ số của tam giác ABD và ACD là \(\frac{m}{n}\)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: BC=căn 12^2+16^2=20cm
c: AD là phân giác
=>BD/CD=AB/AC=3/4
=>S ABD/S ACD=3/4
d: BD/CD=3/4
=>BD/3=CD/4
mà BD+CD=10
nên BD/3=CD/4=10/7
=>BD=30/7cm; CD=40/7cm

Gọi đường cao chung của 2 tam giác ABD và ACD là AH
Xét tam giác ABC có:
AD là đường phân giác
=>\(\dfrac{DB}{DC}=\dfrac{AB}{AC}\)
=>\(\dfrac{DB}{DB+DC}=\dfrac{AB}{AB+AC}\)
=>\(\dfrac{DB}{BC}=\dfrac{6}{6+4}\)
=>\(\dfrac{DB}{5}=\dfrac{6}{10}\)
=>DB=3cm
CMTT:DC=2cm
Ta có:\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{\dfrac{1}{2}.AH.BD}{\dfrac{1}{2}.AH.DC}=\dfrac{BD}{DC}=\dfrac{3}{2}\)
-Xét △ABC có: AD là đường phân giác (gt).
\(\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{6}{4}=\dfrac{3}{2}\) (định lí đường phân giác).
\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{DB}{DC}=\dfrac{3}{2}\)
\(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{BD}{CD}=\dfrac{AB}{AC}=\dfrac{4}{8}=\dfrac{1}{2}\)