Vẽ hộ mình cả hình nữa với! Mình cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Q
2
29 tháng 5 2022
a: Xét ΔBAK và ΔBDK có
BA=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
Do đó: ΔBAK=ΔBDK
b: Ta có: ΔBAK=ΔBDK
nên KA=KD
mà BA=BD
nên BK là đường trung trực của AD
29 tháng 5 2022
a)Xét \(\Delta BAK\) và \(\Delta BDK\) có:
AB=BD
\(\widehat{ABK}=\widehat{DBK}\)
BK chung
=> \(\Delta BAK\) = \(\Delta BDK\) (c-g-c)
b)Gọi O là giao điểm của AD và BK
Xét \(\Delta ABO\) và \(\Delta DBO\) có :
BO chung
\(\widehat{ABO}=\widehat{DBO}\)
AB=DB
=> \(\Delta ABO\) và \(\Delta DBO\) (c-g-c)
=> AO=BO (1) ; \(\widehat{AOB}=\widehat{DOB}\)
Có : \(\widehat{AOB}+\widehat{DOB}=180^o\) mà \(\widehat{AOB}=\widehat{DOB}\)
=> \(\widehat{AOB}=\widehat{DOB}=\dfrac{180^o}{2}=90^o\) (2)
Từ (1)(2) => BK là đường trung trực cùa AD
TC
7 tháng 2 2020
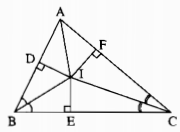
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
\(\eqalign{
& \widehat {I{\rm{D}}B} = \widehat {IEB} = 90^\circ \cr
& \widehat {DBI} = \widehat {EBI}\left( {gt} \right) \cr} \)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng)
Quảng cáo
Xét hai tam giác vuông IEC và IFC, ta có ;
\(\eqalign{
& \widehat {IEC} = \widehat {IFC} = 90^\circ \cr
& \widehat {ECI} = \widehat {FCI}\left( {gt} \right) \cr} \)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
H
7 tháng 2 2020
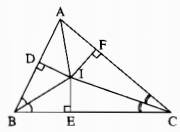
Kẻ: ID⊥AB,IE⊥BC,IF⊥ACID⊥AB,IE⊥BC,IF⊥AC
Xét hai tam giác vuông IDB và IEB, ta có:
ˆIDB=ˆIEB=90∘ˆDBI=ˆEBI(gt)IDB^=IEB^=90∘DBI^=EBI^(gt)
BI cạnh huyền chung
⇒⇒ ∆IDB = ∆IEB (cạnh huyền, góc nhọn)
Suy ra: ID = IE (hai cạnh tương ứng) (1)
Xét hai tam giác vuông IEC và IFC, ta có ;
ˆIEC=ˆIFC=90∘ˆECI=ˆFCI(gt)IEC^=IFC^=90∘ECI^=FCI^(gt)
CI canh huyền chung
Suy ra: ∆ IEC = ∆IFC (cạnh huyền, góc nhọn)
Suy ra: IE = IF (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: ID = IF
Xét hai tam giác vuông IDA và IFA, ta có:
ˆIDA=ˆIFA=90∘IDA^=IFA^=90∘
ID = IF (chứng minh trên)
AI cạnh huyền chung
Suy ra: ∆IDA = ∆IFA (cạnh huyền, cạnh góc vuông)
Suy ra: ˆDAI=ˆFAIDAI^=FAI^ (hai góc tương ứng)
Vậy AI là tia phân giác của ˆA
Read more: https://sachbaitap.com/cau-100-trang-151-sach-bai-tap-sbt-toan-lop-7-tap-1-c7a10140.html#ixzz6DFwdbF2W
3N
Các bạn giải cả 3 bài này giúp mình với, mình đang gấp nhớ vẽ hình lun ạ !!! Cảm ơn
1
12 tháng 2 2022
=)) Mik chịu á, bạn cứ làm mấy chỗ khác trước và chừa chứng minh cho mik cx đc ạ
20 tháng 1
Xét ΔDEF có DE<DF<EF
mà \(\widehat{F};\widehat{E};\widehat{D}\) lần lượt là góc đối diện của các cạnh DE,DF,EF
nên \(\widehat{F}< \widehat{E}< \widehat{D}\)
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
b: Xét ΔAHD vuông tại H và ΔAKE vuông tại K có
AD=AE
\(\widehat{HAD}=\widehat{KAE}\)
Do đó: ΔAHD=ΔAKE
Suy ra: HD=EK
c: Xét ΔABC có
AH/AB=AK/AC
nên HK//BC