Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chưa có ai trả lời câu hỏi này, hãy gửi một câu trả lời để giúp HitRuu Zero giải bài toán này.
Gửi câu trả lời của bạn
Bài 1: Điền vào chỗ trống trong các phát biểu sau
a) Hai đường thẳng vuông góc với nhau là hai đường thẳng ..................................
b) Có ........................ đường thẳng a' đi qua điểm O và vuông góc với đường a cho trước
b) Đường trung trực của đoạn thẳng AB là .............................
Bài 2: Trong các khẳng định sau khẳng định nào đúng, khẳng định nào sai
a) Hai đường thẳng vuông góc thì cắt nhau
b) Hai đường thẳng cắt nhau thì vuông góc
c) Đường thẳng xx' và yy' cắt nhau tạo thành 4 góc vuông
d) Khi 2 đường thẳng xx' và yy' vuông góc với nhau thì mỗi đường thẳng là đường phân giác của 1 góc bẹt.
Bài 3: Cho AB= 6cm. Hãy vẽ đường trung thực của đoạn thẳng AB, nêu cách vẽ.
Bài 4: Vẽ hình theo cách diễn đạt sau:
Vẽ góc xOy có số đo bằng 600. Lấy điểm A bất kì nằm trong góc xOy. Vẽ qua A đường thẳng d1 vuông góc với tia Ox tại B. Vẽ qua A đường thẳng d2 vuông góc với Oy tại C.
Bài 5: Cho đường thẳng d và điểm O nằm ngoài đường thẳng d. Chỉ sử dụng eke hãy vẽ đường thẳng d' đi qua O và vuông góc với d. Nói rõ cách vẽ
Bài 6: vẽ MN= 3cm, NP= 4cm. Hãy vẽ đường trung trực của mỗi đoạn thẳng ấy. Nêu cách vẽ
Bài 7: Trên cùng một nửa mặt phẳng có bờ chứa tia OA, vẽ các tia OB, OC sao cho AOB = 700 , OC vuông góc với OA. Tính số đo góc BOC
Câu hỏi tương tự Đọc thêm
a, ...cắt nhau và trong số các góc tạo thành có một góc bằng 90°
b, ...một...
c, ...là đường thẳng vuông góc với AB tại trung điểm M của đoạn thẳng AB

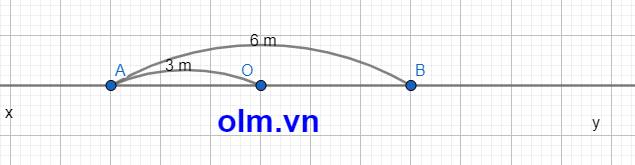
a, Các cặp tia đối nhau chung gốc A lần lượt là:
Ax và AO; Ax và AB; Ax và AY
b, Vì OA và OB là hai tia đối nhau nên O nằm giữa A và B
⇒ OA + OB = AB
⇒ OB = AB - OA
Độ dài đoạn OB là: 6 - 3 = 3 (cm)
c, Vì O nằm giữa A và B mà OA = OB = 3 cm nên O là trrung điểm AB

a: Các cặp tia đối nhau gốc A là:
AB,Ax
AO,Ax
Ay,Ax
b: Trên tia Ay, ta có: AO<AB(3cm<6cm)
nên O nằm giữa A và B
=>AO+OB=AB
=>OB+3=6
=>OB=3(cm)
c: Vì O nằm giữa A và B
và OA=OB(=3cm)
nên O là trung điểm của AB
a) Cặp tia đối nhau gốc A trên hình vẽ là tia OA và tia AO.
b) Độ dài đoạn thẳng OB có thể tính bằng cách sử dụng định lý Pythagoras trong tam giác vuông OAB:
OB² = OA² + AB²
OB² = 3² + 6²
OB² = 9 + 36
OB² = 45
OB = √45 ≈ 6.71 cm
c) Điểm O không phải là trung điểm của đoạn thẳng AB. Để chứng minh điều này, ta có thể tính độ dài của OA và OB:
OA = 3 cm
OB = 6.71 cm
Ta thấy OA ≠ OB, do đó O không là trung điểm của AB.
tick mik nha

Mình nghĩ khó mà có người giải hết chỗ bài tập đấy của bạn, nhiều quá
3/ (Bạn tự vẽ hình giùm)
a/ \(\Delta ABC\)và \(\Delta ADC\)có:
\(\widehat{BAC}=\widehat{ACD}\)(AB // DC; ở vị trí so le trong)
Cạnh AC chung
\(\widehat{CAD}=\widehat{ACB}\)(AB // DC; ở vị trí so le trong)
=> \(\Delta ABC\)= \(\Delta ADC\)(g. c. g)
=> AD = BC (hai cạnh tương ứng)
và AB = DC (hai cạnh tương ứng)
b/ Ta có AD = BC (cm câu a)
và \(AN=\frac{1}{2}AD\)(N là trung điểm AD)
và \(MC=\frac{1}{2}BC\)(M là trung điểm BC)
=> AN = MC
Chứng minh tương tự, ta cũng có: BM = ND
\(\Delta AMB\)và \(\Delta CND\)có:
BM = ND (cmt)
\(\widehat{ABM}=\widehat{NDC}\)(AB // CD; ở vị trí so le trong)
AB = CD (\(\Delta ABC\)= \(\Delta ADC\))
=> \(\Delta AMB\)= \(\Delta CND\)(c. g. c)
=> \(\widehat{BAM}=\widehat{NCD}\)(hai góc tương ứng)
và \(\widehat{BAC}=\widehat{ACN}\)(\(\Delta ABC\)= \(\Delta ADC\))
=> \(\widehat{BAC}-\widehat{BAM}=\widehat{ACN}-\widehat{NCD}\)
=> \(\widehat{MAC}=\widehat{ACN}\)(1)
Chứng minh tương tự, ta cũng có \(\widehat{AMC}=\widehat{ANC}\)(2)
và AN = MC (cmt) (3)
=> \(\Delta MAC=\Delta NAC\)(g, c. g)
=> AM = CN (hai cạnh tương ứng) (đpcm)
c/ \(\Delta AOB\)và \(\Delta COD\)có:
\(\widehat{BAO}=\widehat{OCD}\)(AB // DC; ở vị trí so le trong)
AB = CD (cm câu a)
\(\widehat{ABO}=\widehat{ODC}\)(AD // BC; ở vị trí so le trong)
=> \(\Delta AOB\)= \(\Delta COD\)(g. c. g)
=> OA = OC (hai cạnh tương ứng)
và OB = OD (hai cạnh tương ứng)
d/ \(\Delta ONA\)và \(\Delta MOC\)có:
\(\widehat{AON}=\widehat{MOC}\)(đối đỉnh)
OA = OC (O là trung điểm AC)
\(\widehat{OAN}=\widehat{OCM}\)(AM // NC; ở vị trí so le trong)
=> \(\Delta ONA\)= \(\Delta MOC\)(g. c. g)
=> ON = OM (hai cạnh tương ứng)
=> O là trung điểm MN
=> M, O, N thẳng hàng (đpcm)
x x` y y` O A B t t` C u v D a các tia đối nhau là: aA và Ay; xA và Ax` các tia trùng nhau là: xO và xA; xO và xx`; xA và xx` aA và aC; aA và aC; aA và aB; aA và ay;AC và AB; AC và AB AC và Ay; CB và Cy