Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

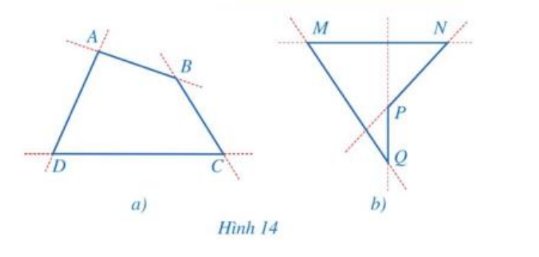
Hình 14a: Tứ giác ABCD luôn nằm về 1 phía của 1 cạnh bất kì.
Hình 14b: Tứ giác MNPQ nằm về 2 phía của đường thẳng chứa cạnh PQ, cạnh NP

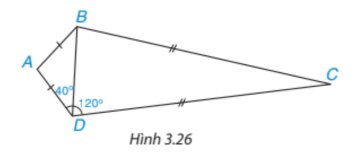
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

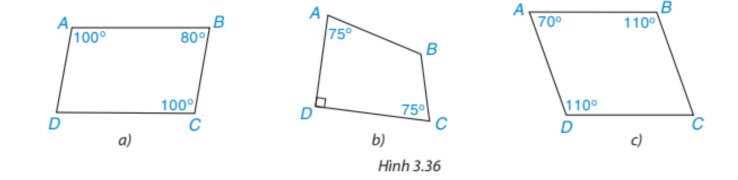
* Hình 3.36a)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
100°+80°+100°+\(\widehat D = {360^o}\)
280°+\(\widehat D\)=360°
Suy ra \(\widehat D\)=360°−280°=80°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100°; \(\widehat B = \widehat D\)=80°
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.36b)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
75°+\(\widehat B\)+75°+90°=360°
240°+\(\widehat B\)=360°
Suy ra \(\widehat B\)=360°−240°=120°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100° nhưng \(\widehat B \ne \widehat D\)(120°≠90°)
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.36c)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
70°+110°+\(\widehat C\)+110°=360°
\(\widehat C\)+290°=360o
Suy ra \(\widehat C\)=360°−290°=70°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=70°; \(\widehat B = \widehat D\)=110°
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.

Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

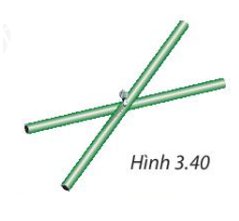
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.

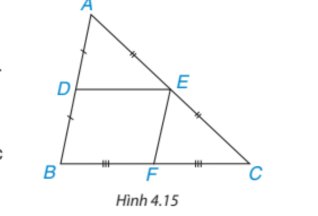
Ta có AD = BD và D ∈ AB nên D là trung điểm của AB;
AE = EC và E ∈ AC nên E là trung điểm của AC.
Xét tam giác ABC có D, E lần lượt là trung điểm của AB và AC, theo định lí Thalès đảo, ta suy ra DE // BC (đpcm).

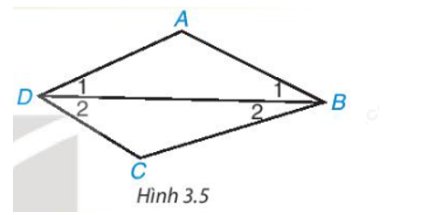
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

Áp dụng định lí về tổng ba góc trong một tam giác đối với tam giác ABD và CBD, ta có:
\(\begin{array}{l}\widehat A + \widehat {{B_1}} + \widehat {{D_1}} = {180^o}\\\widehat C + \widehat {{B_2}} + \widehat {{D_2}} = {180^o}\end{array}\)
Khi đó, tứ giác ABCD có:
\(\widehat A + \widehat B + \widehat C + \widehat D = \widehat A + \widehat {{B_1}} + \widehat {{D_1}} + \widehat C + \widehat {{B_2}} + \widehat {{D_2}} = 180^\circ + 180^\circ = 360^\circ \)
Vậy \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
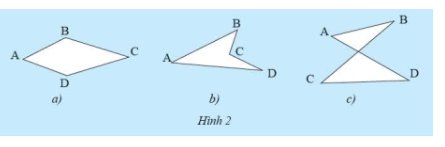
a: Các cạnh còn lại của tứ giác luôn nằm trong cùg một mặt phẳng
b: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc CD) của tứ giác.
c: các cạnh còn lại của tứ giác không nằm trong cùng một mặt phẳng được phân chia bởi đường thẳng chứa cạnh BC (hoặc AD) của tứ giác.