Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) - Trong hình vẽ có tất cả 12 góc
b) - Có 6 cặp góc đối đỉnh ( không kể góc bẹt)

Các góc đối đỉnh trong hình là: \(\widehat {DOB}\) và \(\widehat {COA}\); \(\widehat {BOC}\) và \(\widehat {AOD}\)

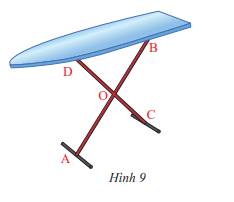
Xét \(\Delta ABD\)và \(\Delta ACD\)có
\(\widehat{ABD}=\widehat{ACD}=90^o\left(BD\perp AB;CD\perp AC\right)\)
AB = AC ( \(\Delta ABC\)cân tại A )
AD: Cạnh chung
Do đó : \(\Delta ABD=\Delta ACD\)( cạnh huyền - cạnh góc vuông )
\(\Rightarrow\widehat{BAD}=\widehat{CAD}\) ( 2 góc tuơng ứng )
Gọi I là giao điểm của BC và AD
Xét \(\Delta ABI\)và \(\Delta ACI\) có:
AB = AC ( tam giác ABC cân ở A )
\(\widehat{BAI}=\widehat{CAI}\left(cmt\right)\)
AI : cạnh chung
Do đó : \(\Delta ABI=\Delta ACI\left(c.g.c\right)\)
\(\Rightarrow BI=CI\)( cặp cạnh tuơng ứng )
Mà \(I\in BC\)
Nên I là trung điểm của BC (1)
Ta có: \(\widehat{AIB}=\widehat{AIC}\)( \(\Delta ABI=\Delta ACI\) )
Mà \(\widehat{AIB}+\widehat{AIC}=180^o\)( 2 góc kề bù )
Nên : \(\widehat{AIB}=\widehat{AIC}=\frac{180^o}{2}=90^o\)
=> \(AI\perp BC\)hay \(AD\perp BC\) (2)
Từ (1) và (2) suy ra : AD là đuờng trung trực của BC ( đpcm )
Xét tam giác ADB và tam giác ADC có
AD chung
góc ABD= góc ACD(=90)
AB=AC(gt)
=>tam giác ADC= tam giác ADC
=>góc BAD=gócCAD
=>AD phan giac goc a
Mà trong một tam giác cân tia phân giac là đường trung trực
=>AH trung trực BC

a) Ba đường thẳng cắt nhau tại O tạo thành 6 tia. Số góc do 6 tia tạo ra là: 6.5 2 = 15 (góc).
b) Xét hai đường thẳng AB và CD trong ba đường thẳng đã cho (h.1.11). Hai đường thẳng này tạo thành bốn góc không có điểm trong chung. Tổng của bốn góc này bằng 360 ° nên trong bốn góc đó phải tồn tại một góc lớn hơn hoặc bằng 90 ° .
Thật vậy, nếu mỗi góc đó đều nhỏ hơn 90 ° thì tổng của chúng nhỏ hơn 90 ° .4 = 360 ° : vô lí.
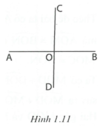
Giả sử góc tồn tại nói trên là góc BOD.
- Nếu B O D ^ > 90 ° thì A O C ^ = B O D ^ > 90 ° , bài toán đã giải xong.
- Nếu B O D ^ = 90 ° thì ta xét tiếp đường thẳng thứ ba MN đi qua O (h.1.12).
Giả sử tia ON nằm trong góc BOD. Khi đó góc BON là góc nhọn do đó A O N ^ là góc tù (vì B O N ^ và A O N ^ là hai góc kề bù). Góc AON là góc tù thì góc BOM là góc tù (vì B O M ^ = A O N ^ ).
Vậy luôn tồn tại hai góc tù trong số 15 góc được tạo thành.
Chứng tỏ hai tia đối nhau