Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Phương pháp:
+) Tính số phần tử của không gian mẫu.
+) Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2". Tìm đẩy đủ các bộ số có hiệu bằng 2.
+) Tính xác suất của biến cố A.
Cách giải:
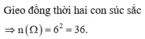
Gọi A là biến cố: "Hiệu số chấm xuất hiện trên các mặt của hai con súc sắc bằng 2".
Các bộ số có hiệu bằng 2 là (1;3); (2;4); (3;5); (4;6)
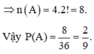

Không gian mẫu: n Ω = 6 . 6 = 36
Gọi A là biến cố: ‘‘Tổng số chấm xuất hiện hai lần tung là một số nhỏ hơn 10’’.
⇒ A ¯ : ‘‘Tổng số chấm xuất hiện hai lần tung là một số không nhỏ hơn 10’’.
Tổng số chấm là một số không nhỏ hơn 10 nên số chấm xuất hiện là các cặp:
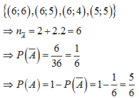
Chọn B.

Đáp án A
Số phần tử của không gian mẫu: n Ω = 6 .6 = 36 .
Gọi A là biến cố mặt 6 chấm không xuất hiện.
Khi đó n A = 5 .5 = 25 ⇒ P A = n A n Ω = 25 36 .

Đáp án B
Gọi B là biến cố cả 3 lần gieo đều xuất hiện số lẻ
⇒ P B = 1 2 . 1 2 . 1 2 = 1 8 (tính chất biến cố độc lập)
Xác suất để tích số chấm 3 lần gieo được số chẵn là 1 − 1 8 = 7 8 .

Số phần tử của không gian mẫu là: n Ω = 6 2 = 36
Gọi A: “tổng số chấm trên mặt xuất hiện của hai con súc sắc đó không vượt quá 5”

Chọn: C
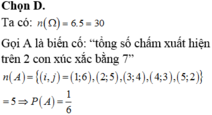



Phương pháp:
Áp dụng công thức nhân xác suất.
Cách giải:
Xác suất để số chấm xuất hiện trên 1 con xúc xắc là số chẵn 1 2
Xác suất để số chấm xuất hiện trên hai con xúc xác đều là số chẵn là 1 2 2 = 1 4
Chọn: C