Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

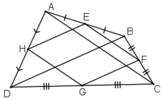
+ E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC
⇒ EF // AC và EF = AC/2
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD
⇒ HG // AC và HG = AC/2.
+ Ta có:
EF //AC, HG//AC ⇒ EF // HG.
EF = AC/2; HG = AC/2 ⇒ EF = HG
⇒ tứ giác EFGH là hình bình hành.

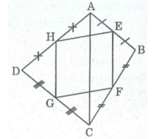
Nối đường chéo AC.
Trong ∆ ABC ta có:
E là trung điểm của AB (gt)
F là trung điểm của BC (gt)
Nên EF là đường trung bình của ∆ ABC
⇒EF//AC và EF = 1/2 AC
(tính chất đường trung hình tam giác) (1)
Trong ∆ ADC ta có:
H là trung điểm của AD (gt)
G là trung điểm của DC (gt)
Nên HG là đường trung bình của ∆ ADC
⇒ HG // AC và HG = 1/2 AC (tính chất đường trung bình tam giác) (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Vậy tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).

 - Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Vì ta nối DB thì sẽ có HE và GF là đường tb của tam giác ADB và DCB => GF//HE vì cùng // với DB và bằng 1/2 DB (1)
- Nối AC thì sẽ có HG và EF là đường tb của tam giác DCA và BAC => EF//HG vì cùng //AC và bằng 1/2 AC (2)
Từ (1) và (2) => tứ giác HEFG là HBH (có các cặp cạnh // và bằng nhau từng đôi một)
=>Hình đó là hình bình hành

Trả lời :
+ E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC
⇒ EF // AC và EF = \(\frac{AC}{2}\)
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD
⇒ HG // AC và HG = \(\frac{AC}{2}\).
+ Ta có:
EF // AC, HG//AC ⇒ EF // HG.
EF = \(\frac{AC}{2}\); HG = \(\frac{AC}{2}\) ⇒ EF = HG
⇒ Tứ giác EFGH là hình bình hành.

Xét \(\Delta ABC\) có:
E là trung điểm AB (gt)
F là trung điểm AC (gt)
=> EF là đường trung bình \(\Delta ABC\) (ĐN đường TB \(\Delta\))
=> EF // AC, \(EF=\dfrac{AC}{2}\) (tính chất đường TB \(\Delta\))
Xét \(\Delta ADC\) có:
H là trung điểm AD
G là trung điểm DC
=> HG là đường trung bình \(\Delta ADC\) (ĐN đường TB \(\Delta\))
=> HG // AC, \(HG=\dfrac{BC}{2}\) (tính chất đường TB \(\Delta\))
Ta có: EF // AC, HG // AC
\(EF=\dfrac{AC}{2},HG=\dfrac{AC}{2}\)
=> EF // HG, EF = HG
Xét tứ giác EFGH có:
EF // HG
EF = HG
=> EFGH là hình bình hành (dhnb)
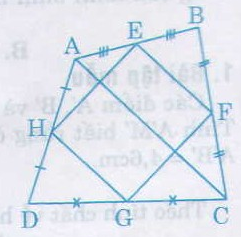
Tứ giác EFGH là hình bình hành.
Cách 1: EB = EA, FB = FC (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
Tương tự HG là đường trung bình của ∆ACD.
Do đó HG // AC
Suy ra EF // HG (1)
Tương tự EH // FG (2)
Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiêu nhận biết 1).
Cách 2: EF là đường trung bình của ∆ABC nên EF = 1212AC.
HG là đường trung bình của ∆ACD nên HG = 1212AC.
Suy ra EF = HG
Lại có EF // HG ( chứng minh trên)
Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3).

Tự vẽ hình :)
t/g ABC có :
AE = EB
BF = FC
\(\Rightarrow\)EF - đường trung bình của tam giác ABC
\(\Rightarrow\)\(EF\)// \(AC\)\(,\)\(EF=\frac{AC}{2}\left(1\right)\)
t/g ADC có :
AH = HD
CG = GD
\(\Rightarrow\)HG - đường trung bình của tam giác ADC
\(\Rightarrow\)\(HG\)// \(AC\)\(,\)\(HG=\frac{AC}{2}\)\(\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Leftrightarrow\)EF // HG , EF = HG
Vì tứ giác EFGH có 2 cạnh đối song song và bằng nhau
\(\Rightarrow\)EFGH - hình bình hành ( đpcm )

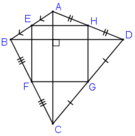
Ta có EB = EA, FB = FC (gt)
⇒ EF là đường trung bình của ΔABC
⇒EF // AC và EF = AC/2 (1)
HD = HA, GD = GC
⇒ HG là đường trung bình của ΔADC
⇒ HG // AC và HG = AC/2 (2)
Từ (1) và (2) suy ra EF // HG và EF = HG
⇒ Tứ giác EFGH là hình bình hành (*)
EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.
Mà EF // AC, AC ⊥ BD
⇒ EH ⊥ EF ⇒ Ê = 90º (**)
Từ (*) và (**) suy ra EFGH là hình chữ nhật.

Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Từ (1) và (2) suy ra EH//FG và EH=FG
Xét ΔABC có
E là trung điểm của AB
F là trung điểm của BC
Do đó: EF là đường trung bình
=>EF//AC
mà AC⊥BD
nên EF⊥BD
mà BD//EH
nên EF⊥EH
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
mà EH⊥EF
nên EHGF là hình chữ nhật
E là trung điểm AB, F là trung điểm BC
⇒ EF là đường trung bình của tam giác ABC
⇒ EF // AC và EF = AC/2
+ H là trung điểm AD, G là trung điểm CD
⇒ HG là đường trung bình của tam giác ACD
⇒ HG // AC và HG = AC/2.
+ Ta có:
EF //AC, HG//AC ⇒ EF // HG.
EF = AC/2; HG = AC/2 ⇒ EF = HG
⇒ tứ giác EFGH là hình bình hành.
Em xem lại đề, em ghi sai đề rồi. Còn bạn Thiện Nhân giải ở dưới thì vẽ hình sai!