Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
a, Có 6 chữ số khác nhau
Gọi số cần tìm là \(\overline{abcdef}\)
a có 5 cách chọn ( \(a\ne0\))
\(\overline{bcedf}\)có 5! cách chọn
=> Có tất cả 5.5! = 600 (số)
Vậy có 600 số có 6 chữ số khác nhau
b, Gọi số có 4 chữ số cần tìm là \(\overline{abcd}\)
Vì \(\overline{abcd}\) là số chẵn nên d \(\in\left(0,2,4\right)\)
TH1: d=0
\(\overline{abc}\) có \(A_5^3\) cách chọn => 60 cách chọn
TH2 : d=(2,4) -> có 2 cách chọn
a có 4 cách chọn ( a khác 0,d)
b có 4 cách chọn ( b khác a,d)
c có 3 cách chọn ( c khác a,b,d)
=> 4.4.3.2=96 số
Nên kết hợp hai trường hợp ta có 60+96=156 ( số)
Vậy có 156 số có 4 chữ số chẵn khác nhau
c, Gọi số có 3 chữ số khác nhau là \(\overline{abc}\)
TH1:
a = {4,5} -> có 2 cách
\(\overline{bc}\) có \(A_4^2\) cách chọn
=> Có 2.\(A_4^2\)=2.12=24 số
TH2: a=3 -> có 1 cách
b={1,2,4,5} -> có 4 cách
c có 4 cách ( c khác a,b)
=> 4.4=16 (số)
TH3: a=3 -> có 1 cách chọn
b=0-> có 1 cách chọn
c={1,2,4,5} -> có 4 cách chọn
=> có 4 số
Nên ta có 24+16+4=44( số)
Vậy có tất cả 44 số có 3 chữ số khác nhau lớn hơn 300

a. Gọi chữ số cần lập là \(\overline{abcd}\)
TH1: \(d=0\Rightarrow\) bộ abc có \(A_9^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 4 cách chọn (từ 2,4,6,8)
a có 8 cách chọn (khác 0 và d), b có 8 cách chọn (khác a và d), c có 7 cách chọn (khác a,b,d)
\(\Rightarrow4.8.8.7\) số
Tổng cộng: \(A_9^3+4.8.8.7=...\)
b. Chọn 4 chữ số còn lại: có \(C_7^4\) cách
Hoán vị 3 chữ số 0,1,2: có \(3!\) cách
Coi bộ 3 chữ số này là 1 số, hoán vị với 4 chữ số còn lại: \(5!\) cách
Ta đi tính số trường hợp 0 đứng đầu:
Số 0 đứng đầu trong bộ 0,1,2: có \(2!\) cách
Đặt bộ 0,1,2 đứng đầu, xếp vị trí cho 4 chữ số còn lại: \(4!\) cách
Vậy có: \(C_7^4.\left(3!.5!-2!.4!\right)=...\) số

1.
Chữ số hàng đơn vị có 4 cách chọn (từ 1,3,5,7)
Chọn và hoán vị 4 chữ số từ 6 chữ số còn lại: \(A_6^4\) cách
Tổng cộng: \(4.A_6^4\) cách
2.
Gọi chữ số cần lập có dạng \(\overline{abcd}\)
a.
Lập số có 4 chữ số bất kì (các chữ số đôi một khác nhau): \(A_6^4\) cách
Lập số có 4 chữ số sao cho số 0 đứng đầu: \(A_5^3\) cách
\(\Rightarrow A_6^4-A_5^3=300\) số
b.
Để số được lập là số chẵn \(\Rightarrow\) d chẵn
TH1: \(d=0\Rightarrow abc\) có \(A_5^3\) cách chọn
TH2: \(d\ne0\Rightarrow d\) có 2 cách chọn (từ 2;4)
a có 4 cách chọn (khác 0 và d), b có 4 cách chọn, c có 3 cách chọn
\(\Rightarrow2.4.4.3=96\) số
Tổng cộng: \(A_5^3+96=156\) số
Xác suất \(P=\dfrac{156}{300}=...\)

Đáp án B
Số đó nhất thiết phải có mặt 3 chữ số 1, 2, 5 ta chỉ cần chọn 2 chữ số nữa từ 4 chữ số còn lại.
TH1: Hai chữ số được chọn kia không chứa số 0: Ta có ![]()
TH2: Hai chữ số kia chứa chữ số 0, ta loại trường hợp chữ số 0 đứng đầu thì còn: 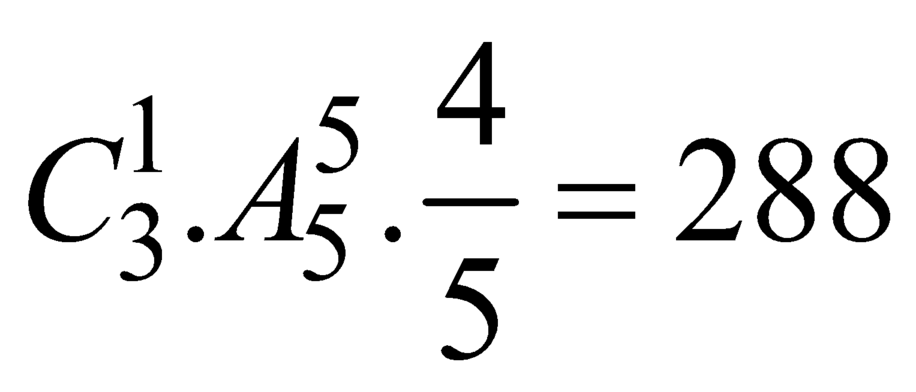
Vậy có tất cả là 648 số

TH1: số 2 đứng đầu:
Chọn 2 chữ số từ 6 chữ số còn lại và hoán vị: \(A_6^2=30\) cách
TH2: số 2 không đứng đầu:
Chọn số hàng trăm: có 5 cách (khác 0 và 2)
Chọn 1 chữ số còn lại: 5 cách, hoán vị nó với 2: có \(2!=2\) cách
\(\Rightarrow5.5.2=50\) cách
Tổng cộng: \(30+50=80\) số

Lời giải:
a. Số số tự nhiên gồm 5 chữ số khác nhau luôn có mặt 1 là:
$5.A^4_6=1800$ (số)
b.
Số số tự nhiên gồm 5 chữ số khác nhau luôn có mặt 1 mà không có 7 là:
$5.A^4_5=600$ (số)
Số số tự nhiên gồm 5 chữ số khác nhau luôn có mặt 1 và 7 là:
$1800-600=1200$ (số)

Đáp án C
Số các số tự nhiên thỏa mãn yêu cầu bài toán là: A 6 4 = 360 số

Chọn B
Mỗi số có ba chữ số khác nhau lập được từ các chữ số 1, 2, 3, 4, 5, 6 là một chỉnh hợp chập 3 của 6 phần tử . Nên số
các số lập được là A 6 3 = 120 .