Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Công thức tính góc lệch đối với lăng kính có góc chiết quang nhỏ và góc tới nhỏ là D = (n – 1)A = 5,20..

Chọn A.
Khoảng cách từ lăng kính tới màn tới là AE = 1m, góc lệch D được tính trong câu 6.19, khoảng cách giữa hai vệt sáng là EM = AE. tanD ≈ AE.D = 9,07 cm.

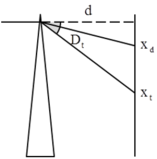
Góc lệch của tia sáng khi qua lăng kính: \(D=(n-1)A\)
Suy ra: \(D_đ=(n_đ-1)A\)
\(D_t=(n_t-1)A\)
Bề rộng quang phổ trên màn: \(DT=HT-HD=IH.\tan D_t -IH.\tan D_đ\)
Khi góc \(\alpha \) rất nhỏ thì \(\tan\alpha\approx\alpha_{rad}\)
\(\Rightarrow DT=IH( D_t -D_đ)=IH.(n_t-n_đ).A\)
\(\Rightarrow DT = 1.(1,68-1,61).\dfrac{8}{180}\pi=0,0122m=1,22cm\)

(xem Hình 24.1G)
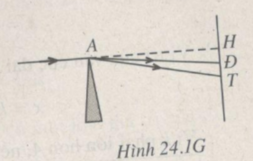
Gọi A là góc chiết quang của lăng kính ;
H là giao điểm của đường kéo dài của tia tới với màn ảnh ; Đ và T là vết của tia đỏ và tia tím trên màn ảnh. Góc lệch của tia đỏ và tia tím là
D đ = A( n đ -1)
D t = A( n t - 1)
Khoảng cách từ các vết đỏ và vết tím đến điểm H là :
HĐ = AH.tan D đ = AH.tanA( n đ - 1)
HT = AH.tan D t = AH.tanA( n t - 1)
Độ rộng từ màu đỏ đến màu tím của quang phổ liên tục trên màn ảnh là :
ĐT = HT - HĐ = AH[tanA( n t - 1) - tanA( n đ - 1)] với A = 6 ° ; n t - 1,685 ; n đ = 1,642 ; AH = 1,2 m thì ĐT = 5,4 mm.

Đáp án: A
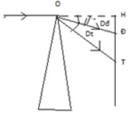
- So với phương tia tới OH, tia đỏ OĐ bị lệch một góc:
Dđ = A(n - 1) = 8.(1,5 - 1) = 4 o
- tia tím OT lệch so với phương OH một góc :
Dt = A.(n - 1) = 8.(1,54 - 1) = 4,32o
Bề rộng quang phổ trên màn là miền ĐT, ta có:
ĐT = TH - ĐH = OH.tanDt - OH.tanDđ = OH.(tan Dt - tan Dđ)
Thay số: ĐT = 1,5.(tan4,32o - tan4o ) = 8,42.10-3 m

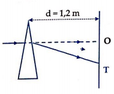

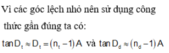
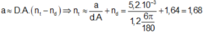
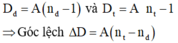
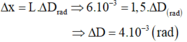
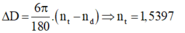
Góc lệch của tia sáng khi qua lăng kính trong trường hợp góc chiết quang nhỏ:
\(D = (n-1).A = (1,65-1).8 = 5,2^0\)
Chọn C