Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
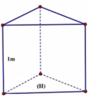
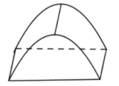
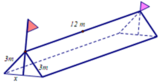
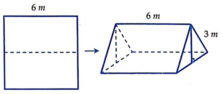
Không gian lều là một khối lăng trụ đứng có chiều cao là 6 m, đáy là tam giác cân có cạnh bên là 3 m và góc ở đỉnh là φ ∈ 0 ; 180 ° .
Khi đó thể tích của khối lăng trụ là: V = 1 3 . 1 2 . 3 . 3 sin φ . 6 = 9 sin φ ( m 3 )
⇒ V m a x ⇔ sin φ m a x ⇒ φ = 90 °
Gọi chiều cao gậy là h ⇒ h = 3 2 2 (m)

Đáp án C
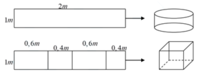
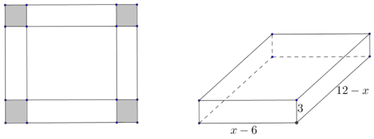
Gọi chiều rộng của hình chữ nhật ban đầu là x(cm), 0<x<18.
⇒ Chiều dài của hình chữ nhật ban đầu là 18-x (cm)
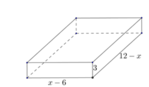
Hình hộp tạo thành có chiều dài là 18-x-6 = 12-x (cm), chiều rộng là x-6 (cm) và chiều cao là 3(cm). Do đó thể tích của hình hộp là


Đáp án B
Gọi chiều rộng của hình chữ nhật ban đầu là x (cm), 0 < x < 18
=> Chiều dài của hình chữ nhật ban đầu là 18 - x(cm)
Hình hộp tạo thành có chiều dài là 18 - x - 6 = 12 - x(cm), chiều rộng là x - 6 (cm) và chiều cao là (3cm). Do thể tích của hình hộp là

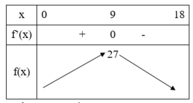
Từ bảng biến thiên suy ra thể tích lớn nhất ![]()

Đáp án B.
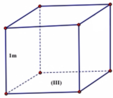
Hình trụ có chu vi đường tròn đáy là C = 12 π ⇒ R = 6 ⇒ S ld = πR 2 = 36 π .
Hình lăng trụ tam giác đều có chu vi đáy là C = 12 π ⇒ a = 4 π ⇒ S 2 d = a 2 3 2 = 8 π 2 3 .
Hình hộp chữ nhật đáy là hình chữ nhật có chu vi đáy là C = 12 π ⇒ a = 2 π b = 4 π ⇒ S 3 d = a . b = 8 π 2 .
Hình hộp chữ nhật đáy là hình vuông có chu vi đáy là C = 12 π ⇒ a = 3 π ⇒ S 4 d = a 2 = 9 π 2 .
So sánh S 2 d > S 1 d ; S 2 d ; S 3 d ; S 4 d ⇒ theo phương án II thì bồ đựng nhiều thóc nhất.

Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
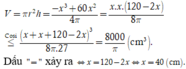
Chọn C.

Chọn A
Phương pháp: Sử dụng công thức thể tích hình trụ và công thức thể tích hình hộp.
Cách giải:


Chọn B.
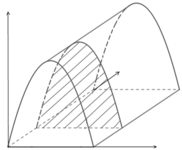
Phương pháp: Sử dụng tích phân.
Cách giải: Chọn hệ trục tọa độ như hình sao cho mặt trước của lều là mặt (Oxy), mặt đáy lều là mặt (Oyz).



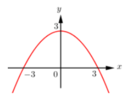
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Gọi phương trình parabol là: y = a x 2 + b x + c


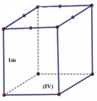
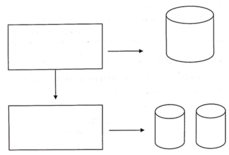
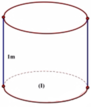
Ban đầu bán kính đáy là R, sau khi cắt và gò ta được 2 khối trụ có bán kính đáy là R 2 . Đường cao của các khối trụ không thay đổi. Ta có:
V 1 = S d h = π . R 2 . h V 2 = 2 S dl . h = 2 π R 2 h = πR 2 h 2
Khi đó: V 1 V 2 = 2
Đáp án C


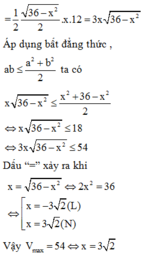

 (I)
(I)