Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi số ngày anh Hải cần phải tiết kiệm là x
Ngày 1 anh hải tiết kiệm được 5000(đồng)
Ngày 2 anh Hải tiết kiệm được 5000+2000(đồng)
Ngày 3 anh Hải tiết kiệm được 5000+2*2000(đồng)
...
Ngày x anh Hải tiết kiệm được 5000+(x-1)*2000(đồng)
Theo đề, ta có:
\(5000+5000+2000+5000+2\cdot2000+...+5000+\left(x-1\right)\cdot2000>=3840000\)
=>\(x\cdot5000+2000\left(1+2+...+x-1\right)>=3840000\)
=>\(5000x+2000\cdot\dfrac{x\left(x-1\right)}{2}>=3840000\)
=>\(5x+\dfrac{2x\left(x-1\right)}{2}>=3840\)
=>\(5x+x^2-x>=3840\)
=>\(x^2+4x-3840>=0\)
=>(x-60)(x+64)>=0
=>\(\left[{}\begin{matrix}x>=60\\x< =-64\left(loại\right)\end{matrix}\right.\)
Vậy; anh hải cần để dành 60 ngày để đủ số tiền mua đôi giày
a) Ta có:
\(\begin{array}{l}{A_0} = 100\\{A_1} = 100 + 100 \times 0,008 - 2 = 98,8\\{A_2} = 98,8 + 98,8 \times 0,008 - 2 = 97,59\\{A_3} = 97,59 + 97,59 \times 0,008 - 2 = 96,37\\{A_4} = 96,37 + 96,37 \times 0,008 - 2 = 95,14\\{A_5} = 95,14 + 95,14 \times 0,008 - 2 = 93,9\\{A_6} = 93,90 + 93,90 \times 0,008 - 2 = 92,65\end{array}\)
Vậy sau 6 tháng số tiền chị Hương còn nợ là 92,65 triệu đồng.
b, Ta có:
\(\begin{array}{l}{A_0} = 100\\{A_1} = {A_0} + {A_0} \times 0,008 - 2 = 1,008{A_0} - 2\\{A_2} = {A_1} + {A_1} \times 0,008 - 2 = 1,008{A_1} - 2\\{A_3} = {A_2} + {A_2} \times 0,008 - 2 = 1,008{A_2} - 2\\...\\ \Rightarrow {A_n} = {A_{n - 1}} + {A_{n - 1}} \times 0,008 - 2 = 1,008{A_{n - 1}} - 2\end{array}\)
Chọn A.
Chọn ngẫu nhiên 5 học sinh trong số 48 học sinh có:
- Gọi A là biến cố "chọn 5 học sinh trong đó có ít nhất một học sinh nữ" thì 
là biến cố "chọn 5 học sinh mà trong đó không có học sinh nữ".
- Ta có số kết quả thuận lợi cho 
là:
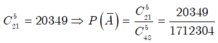
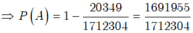
Chọn A
+ Chia đều 10 đội vào 2 bảng A và B có 
cách.
Do đó số phần tử của không gian mẫu là : 
+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.
Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.
Bốn đội còn lại xếp vào bảng còn lại.
Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là 
Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là: 
+ Xác suất cần tìm là: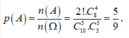 
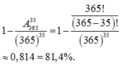
Ngày đầu tiên số tiền thu được là 2000*40=80000(đồng)
Từ ngày thứ hai trở đi thì mỗi ngày sẽ thu được nhiều hơn ngày trước là 500*40=20000(đồng)
Gọi số ngày mà kể từ ngày 1, số tiền quyên góp được đạt 9800000 là x(ngày)(ĐK: x\(\in Z^+\))
Trừ ngày 1 ra thì còn lại là x-1(ngày)
Ngày 1 thu được 80000(đồng)
Ngày 2 thu được 80000+20000(đồng)
Ngày 3 thu được 80000+20000*2(đồng)
...
Ngày x thu được 80000+20000*(x-1)(đồng)
Do đó, ta có: 80000x+(0+20000+20000*2+...+20000*(x-1))>=9800000
=>\(80000x+20000\left(1+2+...+\left(x-1\right)\right)>=9800000\)
=>\(80000x+2000\cdot\dfrac{x\left(x-1\right)}{2}>=9800000\)
=>\(80000x+1000x^2-1000x>=9800000\)
=>\(1000x^2+79000x-9800000>=0\)
=>\(x^2+79x-9800>=0\)
=>\(\left[{}\begin{matrix}x>=\dfrac{-79+9\sqrt{561}}{2}\simeq67,08\\x< =\dfrac{-79-9\sqrt{561}}{2}\left(loại\right)\end{matrix}\right.\)
Vậy: Đến ngày thứ 68 thì số tiền quyên góp được sẽ chạm mốc 9800000 đồng