Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi vận tốc lúc đầu của xe là x (km/h; x > 10), thời gian theo dự định là y (y > 3) (giờ)
Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 3 giờ nên ta có phương trình (x + 10) (y – 3) = xy
Suy ra hệ phương trình :
x − 10 y + 5 = x y x + 10 y − 3 = x y ⇔ − 3 x + 10 y = 30 5 x − 10 y = 50 ⇔ x = 40 y = 15
(thỏa mãn)
Vậy vận tốc ban đầu là 40 km/h
Đáp án: A

Gọi vận tốc xe thứ 2 là x(x>0) km/h
Vận tốc xe thứ nhất là x+10km/h
thời gian xe thứ nhất đi hết quãng đường AB là \(\dfrac{100}{x+10}\)h
thời gian xe thứ 2 đi hết quãng đường AB là \(\dfrac{100}{x}\)h
Vì xe thứ nhất đến B sớm hơn xe thứ 2 là 30p=\(\dfrac{1}{2}\)h nên ta có pt
\(\dfrac{100}{x}\)-\(\dfrac{100}{x+10}\)=\(\dfrac{1}{2}\)
giải pt x=40
vậy vận tốc xe thứ 2 là 40km/h
=> vận tốc xe thứ 2 là 40+10=50 km/h
THAM KHẢO :
Gọi vận tốc của xe thứ nhất a (km/h),
vận tốc của xe thứ hai là là b(km/h) (a>10,b>0)
Vận tốc của xe thiws nhất lớn hơn vận tốc của xe thứ hai là 10km/giờ nên a=b+10(1)
Quãng đường AB dài 100km.
Thời gian đi hết quãng đường AB của xe thứ nhất là 100/a(giờ)
Thời gian đi hết quãng đường AB của xe thứ hai là 100/b (giờ)
Xe thứ nhất đến B sớm hơn xe thứ hai 30 phút=1/2 giờ nên ta có:
100a+12=100b(2)
Thay (1) và (2) ta có:
100b+10+12=100b
⇒100.2.b+b(b+10)=100.2.(b+10)
⇔b2+10b−2000=0
⇔(b−40)(b+50)=0⇔
⇒b=40(nhận) suy ra a=50km/h
Hoặc b=−50b=−50 (loại)
Vậy vận tốc của xe thứ nhất là 50 km/h; vận tốc của xe thứ hai là 40 km/h.
Chúc bạn học tốt![]()

Lời giải:
Gọi vận tốc dự định là $a$ (km/h)
Thời gian dự định: $\frac{AB}{a}$ (giờ)
Thời gian khi xe chạy nhanh hơn dự định 10km/h là: $\frac{AB}{a+10}$ (giờ)
Thời gian khi xe chạy chậm hơn dự định 10km/h là: $\frac{AB}{a-10}$ (giờ)
Theo bài ra ta có:
\(\left\{\begin{matrix} \frac{AB}{a}-\frac{AB}{a+10}=3\\ \frac{AB}{a-10}-\frac{AB}{a}=5\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{10AB}{a(a+10)}=3\\ \frac{10AB}{a(a-10)}=5\end{matrix}\right.\)
Chia theo vế: \(\frac{a(a-10)}{a(a+10)}=\frac{3}{5}\Leftrightarrow \frac{a-10}{a+10}=\frac{3}{5}\Leftrightarrow a=40\) (km/h)
$AB=\frac{3a(a+10)}{10}=\frac{3.40.50}{10}=600$ (km)

Gọi vận tốc lúc đầu của xe là x (km/h; x > 10), thời gian theo dự định là y (y > 3) (giờ)
Quãng đường xe đi được là: x.y (km)
Nếu xe chạy mỗi giờ nhanh hơn 10km thì đến nơi sớm hơn dự định 1 giờ nên ta có phương trình (x + 10) (y – 1) = xy
Nếu xe chạy chậm lại mỗi giờ 5 km thì đến nơi chậm mất 2 giờ nên ta có phương trình (x – 5) (y + 2) = xy
Suy ra hệ phương trình
x + 10 y − 1 = x y x − 5 y + 2 = x y ⇔ x y − x + 10 y − 10 = x y x y + 2 x − 5 y − 10 = x y ⇔ − x + 10 y = 10 2 x − 5 y = 10 ⇔ x = 10 y = 2
(Thỏa mãn)
Vậy vận tốc ban đầu là 10 km/h
Đáp án: C

Đổi \(30\) phút \(=\dfrac{1}{2}\) giờ
Gọi vận tốc xe thứ nhất là x (km/h)
vận tốc xe thứ hai là y (km/h)
ĐK : x,y > 0 ; x >10
Vì mỗi giờ xe thứ nhất đi nhanh hơn xe thứ hai là 10 km nên ta có pt:
\(x-y=10\) (1)
Thời gian xe thứ nhất đi 150 km là: \(\dfrac{150}{x}\) (giờ)
Thời gian xe thứ hai đi 150 km là: \(\dfrac{150}{y}\) (giờ)
Vì xe thứ nhất đến sớm hơn xe thứ hai 30 phút nên ta có pt:
\(\dfrac{150}{y}-\dfrac{150}{x}=\dfrac{1}{2}\) (2)
Từ (1) và (2) ta được hpt:
\(\left\{{}\begin{matrix}x-y=10\\\dfrac{150}{y}-\dfrac{150}{x}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+10\\\dfrac{150}{y}-\dfrac{150}{y+10}=\dfrac{1}{2}\left(\text{3}\right)\end{matrix}\right.\)
Giải pt (3):
\(150\cdot2\left(y+10\right)-150\cdot2y=y\left(y+10\right)\)
\(\Leftrightarrow300y+3000-300y=y^2+10y\)
\(\Leftrightarrow-y^2-10y+3000=0\)
\(\Leftrightarrow\left(y-50\right)\left(y+60\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}y-50=0\\y+60=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=50\left(\text{TM}\right)\\y=-60\left(\text{loại}\right)\end{matrix}\right.\)
Thay y = 50 vào \(x=y+10\Leftrightarrow x=50+10\Leftrightarrow x=60\)
Vậy: vận tốc của xe thứ nhất là 50 km.
vận tốc của xe thứ hai là 60 km.

Đáp án B
Gọi vận tốc của xe thứ nhất là x (km/h) (x > 10).
Vận tốc của xe thứ hai là x – 10 (km/h).
Thời gian xe thứ nhất đi từ A đến B là 50/x (h).
Thời gian xe thứ hai đi từ A đến B là 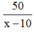 (h).
(h).
Vì xe thứ nhất đến B trước xe thứ hai 15 phút = 1/4 h nên ta có phương trình:
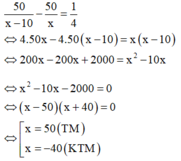
Vậy vận tốc của xe thứ nhất là 50 km/h, vận tốc của xe thứ hai là 40 km/h.