Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lấy M(x; y) thuộc d; gọi M’(x’; y’) là ảnh của M qua phép tịnh tiến theo vecto v → ( 1 ; 0 ) thì
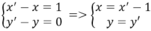
Thay vào phương trình d ta được x’ – 2 = 0, hay phương trình d’ là x – 2 = 0.
Đáp án B
Do \(\overrightarrow{u}\) cùng phương với \(\overrightarrow{i}=\left(1;1\right)\) nên tồn tại một số thực t sao cho \(\overrightarrow{u}=t.\overrightarrow{i}\) ⇒ \(\overrightarrow{u}=\left(t;t\right)\)
d : 3x - y - 7 = 0 nên A (2 ; - 1) ∈ d
Sau khi thực hiện phép tịnh tiến thì ta được điểm B trên d; : 3x - y + 13
thỏa mãn \(\overrightarrow{AB}=\overrightarrow{u}=\left(t;t\right)\)
⇒ B (t + 2 ; t - 1)
Do B ∉ d' ⇒ 3(t + 2) - (t - 1) + 13 = 0
⇒ t = - 10
⇒ Vecto tịnh tiến là \(\overrightarrow{u}=\left(-10;-10\right)\)
biến đường thẳng Δ: x - y -1 = 0 thành đường thẳng Δ' có phương trình là
Giao của d với trục \(Ox\) là điểm \(A\left(3;0\right)\). Phép tịnh tiến phải tìm có vectơ tịnh tiến \(\overrightarrow{v}=\overrightarrow{AO}=\left(-3;0\right)\). Đường thẳng d' song song với d đi qua gốc tọa độ nên nó có phương trình \(3x-y=0\)
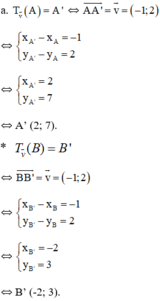
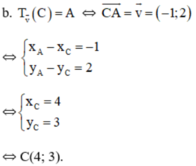
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Giao của d với trục Ox là điểm A(3;0). Phép tịnh tiến phải tìm có vectơ tịnh tiến v → = O A → = ( − 3 ; 0 ) . Đường thẳng d' song song với d và đi qua gốc tọa độ nên nó có phương trình 3x – y = 0.
Vecto chỉ phương của d có tọa độ (3; 1) cùng phương với vecto v→ nên phép tịnh tiến theo vecto v→(3;1) biến đường thẳng d thành chính nó.
Đáp án D