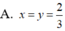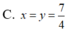Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
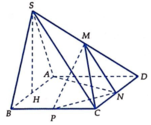
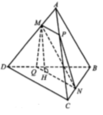
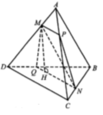
Gọi H là trung điểm của AB. Do ∆ SAB đều nên SH ⊥ AB và
![]()
Mà (SAB) ⊥ (ABCD) nên SH ⊥ (ABCD).
Từ
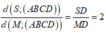
![]()
![]()
Ta có
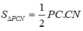
![]()
![]()
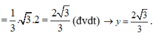
Lại có
![]()
![]()
![]()
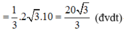
![]()
* Phương án A:
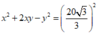
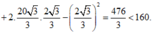
* Phương án B:
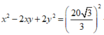
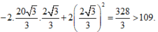
* Phương án C:
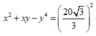
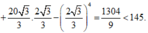
* Phương án D:
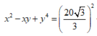
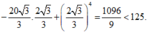

Chọn C
Lời giải. Số các điểm có tọa độ nguyên thuộc hình chữ nhật là 7.3 = 21 điểm vì
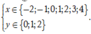
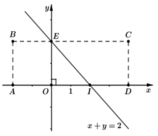
Để con châu chấu đáp xuống các điểm M(x,y) có x + y < 2
thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x,y) có tọa độ nguyên thì
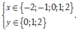
= Nếu x ∈ - 2 ; - 1 thì y ∈ 0 ; 1 ; 2
⇒ có 6 điểm
= Nếu x = 0 thì y ∈ 0 ; 1 ⇒ có 2 điểm
= Nếu x = 1 ⇒ y = 0 ⇒ có 1 điểm
⇒ có tất cả 6 + 2 +1 = 9 điểm thỏa mãn
Vậy xác suất cần tính P = 9 21 = 3 7

Đáp án A
Để con châu chấu đáp xuống các điểm M(x; y) có x + y < 2 thì con châu chấu sẽ nhảy trong khu vực hình thang BEIA
Để M(x; y) có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 , y ∈ { 0 ; 1 ; 2 }
Nếu x ∈ - 2 ; - 1 thì y ∈ { 0 ; 1 ; 2 } có 2.3 = 6 điểm
Nếu x = 0 thì y ∈ { 0 ; 1 } có 2 điểm
Nếu x =1 => y = 0 => có 1 điểm
=> có tất cả 6 + 2 + 1 = 9 điểm. Để con châu chấu nhảy trong hình chữ nhật mà đáp xuống các điểm có tọa độ nguyên thì x ∈ - 2 ; - 1 ; 0 ; 1 ; 2 ; 3 ; 4 , y ∈ { 0 ; 1 ; 2 } . Số các điểm M(x; y) có tọa độ nguyên là: 7.3 = 21 điểm. Xác suất cần tìm là: P = 9 21 = 3 7 .

tham khảo:
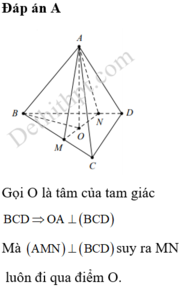
a) Hình chóp S.A1A2...An đều nên SA1 = SA2 = … = SAn
Vì O là hình chiếu của S trên mặt phẳng (A1A2...An) nên OA1, OA2, …, OAn lần lượt là hình chiếu của SA1, SA2, …, SAn
⇒⇒ OA1 = OA2 = … = OAn ⇒⇒ O là tâm đường tròn ngoại tiếp đa giác đáy A1A2...An
b) Nếu đa giác A1A2...An là đều và O là tâm của đa giác đó thì OA1 = OA2 = … = OAn ⇒⇒ SA1 = SA2 = … = SAn ⇒⇒ Hình chóp S.A1A2...An là hình chóp đều