Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì mặt phẳng không đi qua S và song song với mặt phẳng đáy, cắt các cạnh SA1, SA2,.... SAn, tương ứng tại B1, B2,..., Bn nên theo định lý Talet trong từng tam giác SA1A2, …, SAn-1An thì \(\frac{{S{B_1}}}{{S{A_1}}} = \frac{{S{B_2}}}{{S{A_2}}} = \frac{{{B_1}{B_2}}}{{{A_1}{A_2}}} = ... = \frac{{S{B_n}}}{{S{A_n}}}\) mà S.A1A2...An là hình chóp đều nên S.B1B2...Bn cũng là một hình chóp đều.
b) Ta có \(SH \bot \left( {{A_1}{A_2}...{A_n}} \right)\) (H là tâm của đa giác A1A2...An)
Mà \(\left( {{A_1}{A_2}...{A_n}} \right)//\left( {{B_1}{B_2}...{B_n}} \right)\)
\( \Rightarrow \)\(SH \bot \left( {{B_1}{B_2}...{B_n}} \right)\)
Mà \(SK \bot \left( {{B_1}{B_2}...{B_n}} \right)\) (K là tâm của đa giác B1B2...Bn)
\( \Rightarrow \) SH trùng SK
Vậy đường thẳng SH đi qua tâm K của đa giác đều B1B2...Bn, và HK vuông góc với các mặt phẳng (A1A2...An), (B1B2...Bn)

Chọn 3 đỉnh bất kỳ: \(n\left(\Omega\right)=C^3_n\left(cach\right)\)
Gọi 3 đỉnh đó là A,B,C tạo thành tam giác tù =>A >90 độ => B,C<90 độ
Chọn một đỉnh là B (hoặc C): \(C^1_n=n\left(cach\right)\)
Kẻ đường kính ua B chia đường tròn thành 2 nữa, mỗi nữa sẽ có \(\dfrac{n}{2}-1\) (đỉnh của đa giác đều)
Để tạo thành tam giác tù thì A và C (hoặc A và B) phải ở cùng một nữa
Số cách chọn A và C (A và B): \(C^2_{\dfrac{n}{2}-1}+C^2_{\dfrac{n}{2}-1}\left(cach\right)\)
\(\Rightarrow n\left(A\right)=\dfrac{1}{2}.n\left(C^2_{\dfrac{n}{2}-1}+C^2_{\dfrac{n}{2}-1}\right)\left(tam-giac-tu\right)\)
\(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n(\Omega)}=...\)
Làm bừa xem đúng ko :D

Số tam giác có các đỉnh là 3 trong 2n điểm A1;A2;…;A2n là: ![]()
Ta thấy ứng với hai đường chéo đi qua tâm O của đa giác A1A2…A2n cho tương ứng một hình chữ nhật có 4 đỉnh là 4 điểm trong 2n điểm A1;A2;…;A2n và ngược lại mỗi hình chữ nhật như vậy sẽ cho tương ứng hai đường chéo đi qua tâm O của đa giác.
Mà số đường chéo đi qua tâm của đa giác là n nên số hình chữ nhật có đỉnh là 4 trong 2n điểm bằng ![]()
Theo giả thiết: ![]()
⇒n=8.
Chọn C

Chọn D
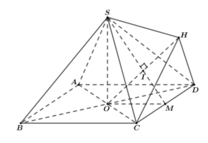
Khối đa diện ABCDSH được chia thành hai khối chóp S.ABCD và H.SCD

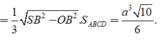
Vì H là điểm đối xứng của O qua SM nên
![]()

Vậy thể tích khối đa diện cần tính bằng
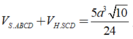

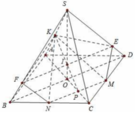
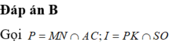
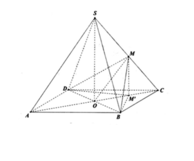
Do MN//BD nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD,SB lần lượt tại E và F khi đó thiết diện là ngũ giác KEMNF






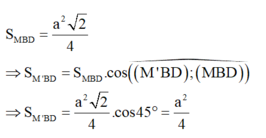
tham khảo:
a) Hình chóp S.A1A2...An đều nên SA1 = SA2 = … = SAn
Vì O là hình chiếu của S trên mặt phẳng (A1A2...An) nên OA1, OA2, …, OAn lần lượt là hình chiếu của SA1, SA2, …, SAn
⇒⇒ OA1 = OA2 = … = OAn ⇒⇒ O là tâm đường tròn ngoại tiếp đa giác đáy A1A2...An
b) Nếu đa giác A1A2...An là đều và O là tâm của đa giác đó thì OA1 = OA2 = … = OAn ⇒⇒ SA1 = SA2 = … = SAn ⇒⇒ Hình chóp S.A1A2...An là hình chóp đều