Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi R là bán kính của đường tròn (C)
(C) và C1 tiếp xúc ngoài với nhau, cho ta:
MF1 = R1+ R (1)
(C) và C2 tiếp xúc ngoài với nhau, cho ta:
MF2 = R2 – R (2)
Từ (1) VÀ (2) ta được
MF1 + MF2 = R1+ R2= R không đổi
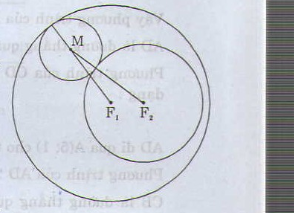
Điểm M có tổng các khoảng cách MF1 + MF2 đến hai điểm cố định F1 và F2 bằng một độ dài không đổi R1+ R2
Vậy tập hợp điểm M là đường elip, có các tiêu điểm F1 và F2 và có tiêu cực :
F1 .F2 = R1+ R2

+) Từ phương trình \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_1}} \) là \(\left( {{a_1};{b_1}} \right)\)
+) Từ phương trình \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\) ta xác định được tọa độ của vectơ \(\overrightarrow {{n_2}} \) là \(\left( {{a_2};{b_2}} \right)\)
+) \(\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \frac{{\overrightarrow {{n_1}} .\overrightarrow {{n_2}} }}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{{a_1}{a_2} + {b_1}{b_2}}}{{\sqrt {{a_1}^2 + {b_1}^2} \sqrt {{a_2}^2 + {b_2}^2} }}\)

1.
\(\left(C_1\right):\left(x-5\right)^2+y^2=25\Rightarrow\) Tâm \(I_1=\left(5;0\right);R_1=5\)
\(\left(C_2\right):\left(x+2\right)^2+\left(y-1\right)^2=25\Rightarrow\) Tâm \(I_2=\left(-2;1\right);R_2=5\)
2.
\(I_1I_2=\sqrt{\left(-2-5\right)^2+\left(1-0\right)^2}=5\sqrt{2}>R_1\)
\(\Rightarrow\) 2 đường tròn ngoài nhau

I(x,y) có tung độ dương nên y>0 và thuộc (d)
nên I(x;-3x-4)
y>0
=>-3x-4>0
=>-3x>4
=>x<-4/3
Theo đề, ta có: d(I;Ox)=d(I;Oy)=R
(C) tiếp xúc với Ox,Oy nên |x|=|-3x-4|
=>3x+4=x hoặc -3x-4=x
=>2x=-4 hoặc -4x=4
=>x=-2(nhận) hoặc x=-1(loại)
=>I(-2;2)
R=|2|=2
=>(C): (x+2)^2+(y-2)^2=4
=>B






