Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
Gọi AH là đường cao của tam giác ABC ⇒ AH ⊥ BC.
B(4;5), C(-3;2) 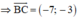
Phương trình đường cao AH đi qua A(2;-1) nhận 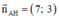 là VTPT là:
là VTPT là:
7.(x - 2) + 3.(y + 1) = 0 ⇔ 7x - 14 + 3y + 3 = 0 ⇔ 7x + 3y - 11 = 0
Vậy phương trình đường cao AH là 7x + 3y - 11 = 0.

Đường cao AH đi qua điểm \(A\left( { - 1;5} \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{AH}}} = \overrightarrow {BC} = \left( {4; - 2} \right)\).
Phương trình tổng quát của AH là \(4\left( {x + 1} \right) - 2\left( {y - 5} \right) = 0 \Leftrightarrow 2x - y + 7 = 0\).

Gọi đường trung tuyến kẻ từ `A` cắt `BC` tại `M`
`=>M` là trung điểm của `BC`
`=>M(2 ; 0)`
Ta có: `\vec{AM} = ( 1 ; -1)` là vtcp của `AM`
`=>\vec{n_[AM]} = ( 1 ; 1 )`
Mà `M(2 ; 0) in AM`
`=>` Pt của đường trung tuyến kẻ từ `A` là:
`1 ( x - 2) + 1 ( y - 0)=0`
`<=> x + y - 2 = 0`

a: (d): 2x-y+3=0
=>y=2x+3
Vì (d') vuông góc với (d) nên 2a=-1
=>a=-1/2
Vậy: (d'): y=-1/2x+b
Thay x=3 và y=1 vào (d'), ta được:
b-3/2=1
hay b=5/2
Vậy: (d'): y=-1/2x+5/2
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x+3=-\dfrac{1}{2}x+\dfrac{5}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-\dfrac{1}{2}\\y=2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{5}\\y=-\dfrac{2}{5}+3=\dfrac{13}{5}\end{matrix}\right.\)

a) Đường cao kẻ từ A của tam giác ABC là đường thẳng đi qua A và có vectơ pháp tuyến là \(\overrightarrow {BC} = \left( { - 5; - 1} \right)\) nên phương trình đường cao đó là:
\( - 5\left( {x - 1} \right) - 1\left( {y - 2} \right) = 0 \Leftrightarrow -5x - y + 7 = 0\)
Hay \( 5x + y - 7 = 0\)
b) Gọi M là trung điểm AC. Khi đó \(\left\{ \begin{array}{l}{x_M} = \frac{{{x_A} + {x_C}}}{2} = \frac{{1 + \left( { - 2} \right)}}{2} = - \frac{1}{2}\\{y_M} = \frac{{{y_A} + {y_C}}}{2} = \frac{{2 + \left( { - 1} \right)}}{2} = \frac{1}{2}\end{array} \right. \Rightarrow M\left( { - \frac{1}{2};\frac{1}{2}} \right)\)
Trung tuyến BM đi qua điểm \(B\left( {3;0} \right)\) nhận vectơ \(\overrightarrow {{u_{BM}}} = 2\overrightarrow {BM} = \left( { - 7;1} \right)\) là vectơ chỉ phương nên phương trình tham số của BM là \(\left\{ \begin{array}{l}x = 3 - 7t\\y = t\end{array} \right.\).