Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Thay x=1 và y=-2 vào y=ax+1, ta được:
a+1=-2
hay a=-3
Vậy: (d'): y=-3x+1
c: Tọa độ giao điểm của (d) và (d') là:
\(\left\{{}\begin{matrix}-3x+1=x+3\\y=x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=3-\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)

a) \(\left\{{}\begin{matrix}\left(d\right):y=-2x-5\\\left(d'\right):y=-x\end{matrix}\right.\)
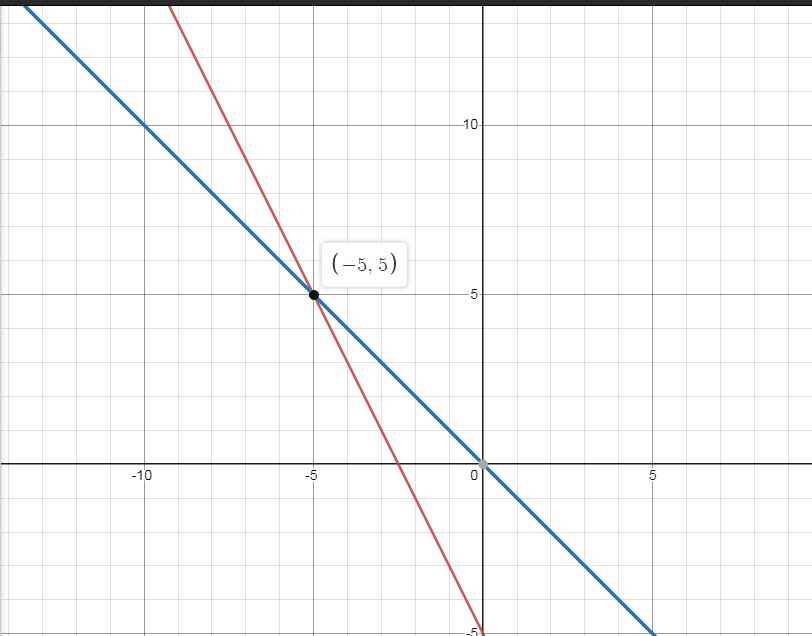
b) \(\left(d\right)\cap\left(d'\right)=M\left(x;y\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=-2x-5\\y=-x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-5\\y=5\end{matrix}\right.\)
\(\Rightarrow M\left(-5;5\right)\)
c) Gọi \(\widehat{M}=sđ\left(d;d'\right)\)
\(\left(d\right):y=-2x-5\Rightarrow k_1-2\)
\(\left(d'\right):y=-x\Rightarrow k_1-1\)
\(tan\widehat{M}=\left|\dfrac{k_1-k_2}{1+k_1.k_2}\right|=\left|\dfrac{-2+1}{1+\left(-2\right).\left(-1\right)}\right|=\dfrac{1}{3}\)
\(\Rightarrow\widehat{M}\sim18^o\)
d) \(\left(d\right)\cap Oy=A\left(0;y\right)\)
\(\Leftrightarrow y=-2.0-5=-5\)
\(\Rightarrow A\left(0;-5\right)\)
\(OA=\sqrt[]{0^2+\left(-5\right)^2}=5\left(cm\right)\)
\(OM=\sqrt[]{5^2+5^2}=5\sqrt[]{2}\left(cm\right)\)
\(MA=\sqrt[]{5^2+10^2}=5\sqrt[]{5}\left(cm\right)\)
Chu vi \(\Delta MOA:\)
\(C=OA+OB+MA=5+5\sqrt[]{2}+5\sqrt[]{5}=5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)\left(cm\right)\)
\(\Rightarrow p=\dfrac{C}{2}=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}\left(cm\right)\)
\(\Rightarrow\left\{{}\begin{matrix}p-OA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5=\dfrac{5\left(\sqrt[]{2}+\sqrt[]{5}-1\right)}{2}\\p-OB=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{2}=\dfrac{5\left(-\sqrt[]{2}+\sqrt[]{5}+1\right)}{2}\\p-MA=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}-5\sqrt[]{5}=\dfrac{5\left(\sqrt[]{2}-\sqrt[]{5}+1\right)}{2}\end{matrix}\right.\)
\(p\left(p-MA\right)=\dfrac{5\left(1+\sqrt[]{2}+\sqrt[]{5}\right)}{2}.\dfrac{5\left(1+\sqrt[]{2}-\sqrt[]{5}\right)}{2}\)
\(\Leftrightarrow p\left(p-MA\right)=\dfrac{25\left[\left(1+\sqrt[]{2}\right)^2-5\right]}{4}=\dfrac{25.2\left(\sqrt[]{2}-1\right)}{4}=\dfrac{25\left(\sqrt[]{2}-1\right)}{2}\)
\(\left(p-OA\right)\left(p-OB\right)=\dfrac{25\left[5-\left(\sqrt[]{2}-1\right)^2\right]}{4}\)
\(\Leftrightarrow\left(p-OA\right)\left(p-OB\right)=\dfrac{25.2\left(\sqrt[]{2}+1\right)}{4}=\dfrac{25\left(\sqrt[]{2}+1\right)}{4}\)
Diện tích \(\Delta MOA:\)
\(S=\sqrt[]{p\left(p-OA\right)\left(p-OB\right)\left(p-MA\right)}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25\left(\sqrt[]{2}-1\right)}{2}.\dfrac{25\left(\sqrt[]{2}+1\right)}{2}}\)
\(\Leftrightarrow S=\sqrt[]{\dfrac{25^2}{2^2}}=\dfrac{25}{2}=12,5\left(cm^2\right)\)

1: Khi m=2 thì y=(2-1)x+2=x+2
Vẽ đồ thị:
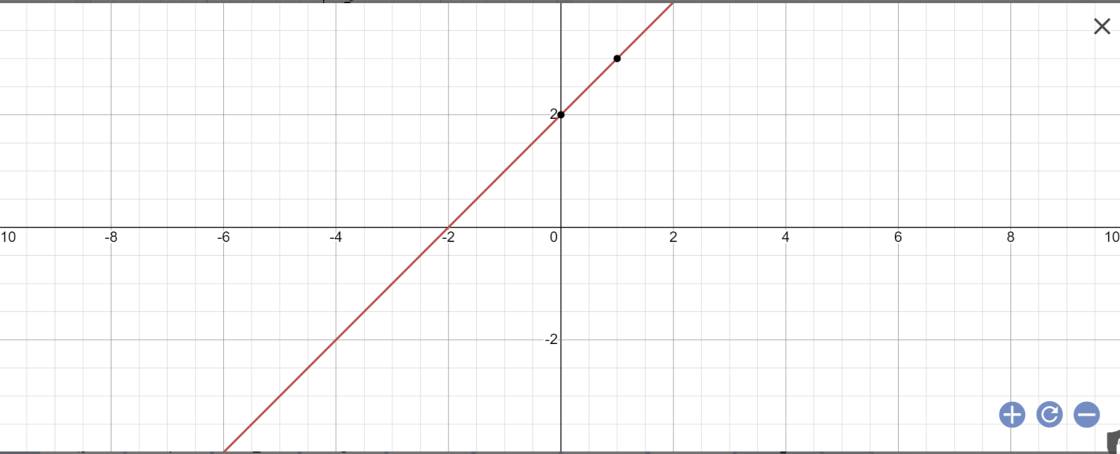
\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
2: Thay x=1 và y=0 vào (d), ta được:
\(1\left(m-1\right)+m=0\)
=>2m-1=0
=>m=1/2
3:
y=(m-1)x+m
=mx-x+m
=m(x+1)-x
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}x+1=0\\y=-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)

a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)

b: Phương trình hoành độ giao điểm là:
\(3x-3=5x+2\)
\(\Leftrightarrow-2x=5\)
\(\Leftrightarrow x=-\dfrac{5}{2}\)
\(\Leftrightarrow y=3\cdot\dfrac{-5}{2}-3=\dfrac{-15}{2}-\dfrac{6}{2}=-\dfrac{21}{2}\)
a: Phương trình hoành độ giao điểm là:
\(x+2=x\sqrt{3}\)
\(\Leftrightarrow x\cdot\left(1-\sqrt{3}\right)=-2\)
\(\Leftrightarrow x=\sqrt{3}+1\)
Thay \(x=\sqrt{3}+1\) vào (d'), ta được:
\(y=\sqrt{3}\left(\sqrt{3}+1\right)=3+\sqrt{3}\)