Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là trọng tâm tam giác ABC \(\Rightarrow G\left(2;1;0\right)\)
\(T=MA^2+MB^2+MC^2\)
\(T=\left(\overrightarrow{MG}+\overrightarrow{GA}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GB}\right)^2+\left(\overrightarrow{MG}+\overrightarrow{GC}\right)^2\)
\(T=3MG^2+GA^2+GB^2+GC^2+2\overrightarrow{MG}\left(\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}\right)\)
\(T=3MG^2+GA^2+GB^2+GC^2\)
Do \(GA^2+GB^2+GC^2\) cố định nên \(T_{min}\) khi \(MG_{min}\)
\(\Rightarrow M\) là hình chiếu vuông góc của G lên (P)
Gọi (d) là đường thẳng qua G và vuông góc (P) \(\Rightarrow\) pt (d): \(\left\{{}\begin{matrix}x=2+t\\y=1+t\\z=t\end{matrix}\right.\)
M là giao điểm (d) và (P) nên thỏa mãn:
\(2+t+1+t+t=0\Leftrightarrow t=-1\) \(\Rightarrow M\left(1;0;-1\right)\)

Chọn D
Giả sử A (a; 0; 0), B (0; b; 0), C (0; 0; c) với a, b, c > 0
Khi đó mặt phẳng (P) có dạng ![]() .
.
Vì (P) đi qua M nên 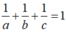
Mặt khác OA = 2OB nên a = 2b nên ![]()
Thể tích khối tứ diện OABC là: V= abc/6
Ta có:
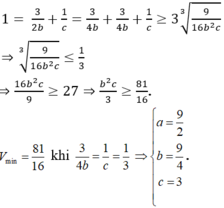

Giống bài trước \(\Rightarrow B'\left(0;2;3\right)\Rightarrow M\left(\dfrac{1}{2};1;\dfrac{3}{2}\right)\)

Mặt cầu (S) cần tìm có tâm I là trung điểm của AB, với I(2;3;0)
Bán kính của (S) là \(R=\frac{AB}{2}=\sqrt{3}\)
Phương trình của (S) : \(\left(x-2\right)^2+\left(y-3\right)^2+z^2=3\)
Gọi \(M\left(0;0;t\right)\in Oz\)
Do \(V_{MABC}=5\) nên \(\frac{1}{6}\left|\left[\overrightarrow{AB},\overrightarrow{AC}\right]\overrightarrow{AM}\right|=5\Leftrightarrow\left|11+4t\right|=5\)
\(\Leftrightarrow\left|11=4t\right|=15\Leftrightarrow\begin{cases}11+4t=15\\11+4t=-15\end{cases}\)
\(\Leftrightarrow\begin{cases}t=1\Rightarrow M\left(0;0;1\right)\\t=-\frac{13}{2}\Rightarrow M\left(0;0;-\frac{13}{2}\right)\end{cases}\)

Chọn D
Gọi A (a;0;0), B (0;b;0), C (0;0;c), do A, B, C thuộc ba tia Ox, Oy, Oz nên a, b, c > 0.

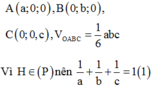

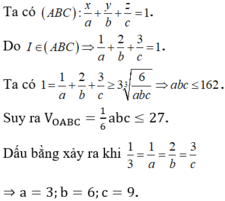
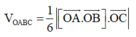
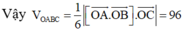
Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
Từ giả thiết
áp dụng bất đẳng thức AM- GM ta có
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
=> (B'C'D') song song với (BCD) và đi qua điểm B'
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
Vậy phương trình (B'C'D') là: