Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính cos(Δ1;Δ2), ta cần tìm vector chỉ phương của hai đường thẳng Δ1 và Δ2.
Vector chỉ phương của đường thẳng d là (1, t, 2) và vector chỉ phương của đường thẳng d' là (-1, 1, -2).
Để tìm vector chỉ phương của mặt phẳng (P), ta lấy vector pháp tuyến của mặt phẳng. Ta có vector pháp tuyến của mặt phẳng (P) là (1, 1, -1).
Để hai đường thẳng Δ1 và Δ2 song song với mặt phẳng (P), ta có điều kiện là vector chỉ phương của Δ1 và Δ2 cũng phải song song với vector pháp tuyến của mặt phẳng (P). Vì vậy, ta cần tìm vector chỉ phương của Δ1 và Δ2 sao cho chúng song song với vector (1, 1, -1).
Ta có thể tìm vector chỉ phương của Δ1 và Δ2 bằng cách lấy tích vector của vector chỉ phương của d hoặc d' với vector pháp tuyến của mặt phẳng (P).
Tính tích vector của (1, t, 2) và (1, 1, -1): (1, t, 2) x (1, 1, -1) = (t-3, 3t+1, -t-1)
Tính tích vector của (-1, 1, -2) và (1, 1, -1): (-1, 1, -2) x (1, 1, -1) = (-1, -3, -2)
Hai vector trên là vector chỉ phương của Δ1 và Δ2. Để tính cos(Δ1;Δ2), ta sử dụng công thức:
cos(Δ1;Δ2) = (Δ1.Δ2) / (|Δ1|.|Δ2|)
Trong đó, Δ1.Δ2 là tích vô hướng của hai vector chỉ phương, |Δ1| và |Δ2| là độ dài của hai vector chỉ phương.
Tính tích vô hướng Δ1.Δ2: (t-3)(-1) + (3t+1)(-3) + (-t-1)(-2) = -t-3
Tính độ dài của Δ1: |Δ1| = √[(t-3)² + (3t+1)² + (-t-1)²] = √[11t² + 2t + 11]
Tính độ dài của Δ2: |Δ2| = √[(-1)² + (-3)² + (-2)²] = √[14]
Vậy, cos(Δ1;Δ2) = (-t-3) / (√[11t² + 2t + 11] * √[14])
Để tính giá trị của cos(Δ1;Δ2), ta cần biết giá trị của t. Tuy nhiên, trong câu hỏi không cung cấp giá trị cụ thể của t nên không thể tính được giá trị chính xác của cos(Δ1;Δ2).

Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
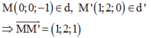
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
![]()
Phương trình mặt phẳng
![]()

Đáp án A
Vì hai đường thẳng d và d’ song song với nhau nên đường thẳng a cần tìm cũng song song với 2 đường thẳng nên a nhận u ⇀ =(3;1;-2) làm vecto chỉ phương.
Gọi A(2;-3;4) ∈ d ⇒ phương trình mặt phẳng (P) qua A vuông góc với d là: 3x+y-2z+5=0
Giao điểm H của (P) và d’ là H 4 7 ; - 15 7 ; - 16 7 . khi đó trung điểm của AH là I 9 7 ; - 18 7 ; 6 7
Thay tọa độ điểm I vào xem phương trình nào thỏa mãn.

Chọn C.
Đường thẳng d có VTCP u → = 2 ; 1 ; 4 và đi qua M(1;7;3).
Đường thẳng d’ có VTCP u ' → = 3 ; - 2 ; 1 và đi qua N(6;-1;-2).

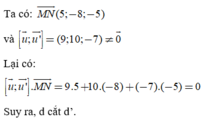

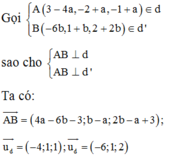


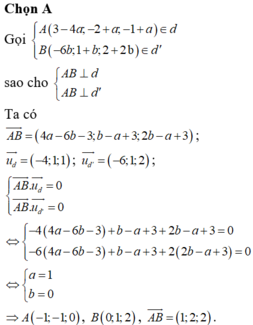

Đáp án A.
Đường thẳng d qua điểm M(2;-2;1) và có vectơ chỉ phương u → = ( - 3 ; 1 ; - 2 )
Đường thẳng d' qua điểm N(0;4;2) và có vectơ chỉ phương u ' → = 6 ; - 2 ; 4
Ta có - 3 6 = 1 - 2 = - 2 4 nếu u → , u ' → cùng phương. Lại có M 2 ; - 2 ; - 1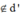
Vậy d ∥ d '