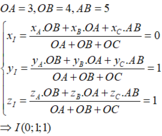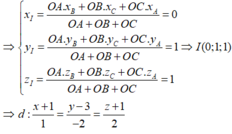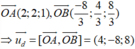Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
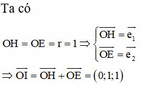
Gọi I là tâm đường tròn nội tiếp tam giác OAB
OA = 3, OB = 4, AB = 5
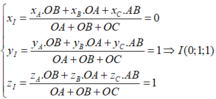

Đáp án A
Do đó O A ¯ ; O B ¯ = - 4 1 ; 1 ; 1 ⇒ O A B : x + y + z = 0
Ta có: I O = I A I O = I B I ∈ O A B ⇒ a 2 + b 2 + c 2 = a 2 + b - 2 2 + c + 2 2 a 2 + b 2 + c 2 = a - 2 2 + b - 2 2 + c + 4 2 a + b + c = 0 ⇔ a = 2 b = 0 c = - 2
Do đó T = a 2 + b 2 + c 2 = 8 .

Đáp án C
Tam giác OAB vuông tại O nên tâm đường tròn ngoại tiếp là trung điểm cạnh AB, tức điểm P(2;0;-1).

Đáp án B
Phương pháp giải:
Tâm đường tròn ngoại tiếp cách đều 3 đỉnh của tam giác và thuộc mặt phẳng chứa tam giác
Lời giải:
Ta có A B → = ( 2 ; 2 ; 1 ) A C → = ( 1 ; 4 ; 3 ) ⇒ A B → ; A C → = ( 2 ; - 5 ; 6 ) => Phương trình (ABC): 2x – 5y + 6z – 10 = 0
Vì I(a;b;c) là tâm đường tròn ngoại tiếp ∆ABC 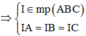
Lại có 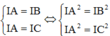
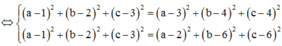
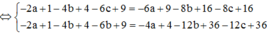
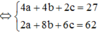
Kết hợp với ![]()
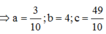 . Vậy S =
46
5
. Vậy S =
46
5