Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
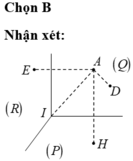
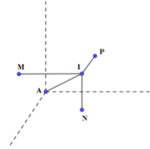
Cho ba mặt phẳng đôi một vuông góc với nhau (P), (Q), (R) tại I. Hạ AH, AD, AE lần lượt vuông góc với ba mặt phẳng trên thì ta luôn có: IA²=AD²+AH²+AE².
Chứng minh:
Chọn hệ trục tọa độ với I (0;0;0), ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng (P), (Q), (R).
Khi đó A (a, b, c) thì IA²=a²+b²+c²=d² (A, (Iyz))+d² (A, (Ixz))+d² (A, (Ixy)) hay IA²=AD²+AH²+AE² #đpcm~.
Áp dụng:
Mặt cầu (S) có tâm I (1;-1;2) và có bán kính r=4 ; 
Gọi và ri là tâm và bán kính của các đường tròn I = 1;2;3
Ta có tổng diện tích các đường tròn là
Đáp án B.
Gọi R1,R2,R3 lần lượt là bán kính của đường tròn giao tuyến.
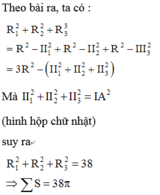
Đáp án C.
Mặt cầu S : x - 1 2 + y - 1 2 + z + 2 2 = 4 có tâm và bán kính R = 2
Xét ba mặt phẳng thay đổi đi qua A và đôi một vuông góc với nhau, cắt mặt cầu (S) theo ba giao tuyến là các đường tròn (C1), (C2), (C3 ) lần lượt là
Gọi r1, r2, r3 lần lượt là bán kính của các đường tròn giao tuyến của mặt cầu (S) với ba mặt phẳng (P1), (P2), (P3 )
Vì (P1), (P2) đi qua tâm I(1;1;-2) nên
nên
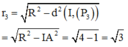
Tổng diện tích của ba hình tròn (P1), (P2), (P3 ) là
Chọn A
Gọi 
là một vec tơ pháp tuyến của mặt phẳng (P).
Theo đề bài ta có mặt phẳng (P) vuông góc với mặt phẳng (α): x-y+z-4=0 nên ta có phương trình a-b+c=0 ó b=a+c 
Phương trình mặt phẳng (P) đi qua A(0;1;2) và có véc tơ pháp tuyến là ax+ (a+c) (y-1)+c (z-2) =0
Khoảng cách từ tâm I (3;1;2) đến mặt phẳng (P) là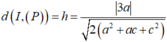 
Gọi r là bán kính của đường tròn giao tuyến giữa mặt cầu (S) và mặt phẳng (P) ta có r²=16-h² ; r nhỏ nhất khi h lớn nhất.
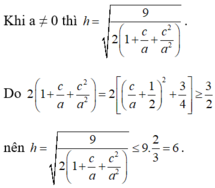
Dấu “=” xảy ra khi a = -2c. => một véc tơ pháp tuyến là 
=> phương trình mặt phẳng (P) là 2x+y-z+1=0.
Vậy tọa độ giao điểm M của (P) và trục x'Ox là: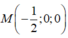 
Đáp án A
Vì mặt phẳng (P) đi qua A, B nên
3 a - 2 b + 6 c - 2 = 0 b = 2 ⇔ a = 2 - 2 c b = 2 ⇒ ( P ) : ( 2 - 2 c ) x + 2 y + c z = 0
Khoảng cách từ tâm I (1;2;3) của (S) đến (P) là:
d(I,(P))= ( 2 - 2 c ) + 2 . 2 + c . 3 - 2 ( 2 - 2 c ) 2 + 2 2 + c 2 = c + 4 5 c 2 - 8 c + 8
Khi đó bán kính của đường tròn giao tuyến là:
r= 25 - ( c + 4 ) 2 5 c 2 - 8 c + 8 = 124 c 2 - 208 c + 184 5 c 2 - 8 c + 8
Để r đạt giá trị nhỏ nhất thì hàm số
f(t)= 124 t 2 - 208 t + 184 5 t 2 - 8 t + 8 trên [1;+ ∞ ) phải nhỏ nhất
Ta có: f'(t)= 48 t 2 + 144 t - 192 ( 5 t 2 - 8 t + 8 ) 2 ,
f'(t)=0
⇔
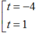
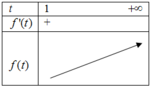
Khi đó hàm số đạt giá trị nhỏ nhất tại t=1 ⇒ c=1
Ta có: T=a+b+c=2-2c+2=4-c=3
Đáp án:
B . ( x + 2 ) 2 + ( y − 1 ) 2 + z 2 = 4
Giải thích các bước giải:
Mặt cầu ( S ) có tâm I ( a ; b ; c ) và bán kính R có phương trình:
( S ) : ( x − a ) 2 + ( y − b ) 2 + ( z − c ) 2 = R 2
Áp dụng:
Mặt cầu ( S ) có tâm I ( − 2 ; 1 ; 0 ) và bán kính R = 2 có phương trình:
( S ) : ( x + 2 ) 2 + ( y − 1 ) 2 + z 2 = 4
Chọn B
Mặt cầu (S): (x-1)²+ (y-2)²+ (z-3)²=9 có tâm I (1;2;3), bán kính R=3.
IA = √6 < R nên A nằm trong mặt cầu.
Gọi r là bán kính đường tròn thiết diện, ta có 
Trong đó h là khoảng cách từ I đến (P).
Diện tích thiết diện là
Vậy diện tích hình tròn (C) đạt nhỏ nhất khi h = IA. Khi đó 
là véc tơ pháp tuyến của (P).
Phương trình mặt phẳng (P) là 1 (x-0)+2 (y-0)+ (z-2)=0 ó x + 2y + z – 2 = 0
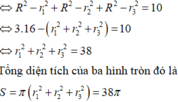
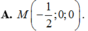
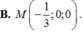
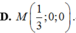
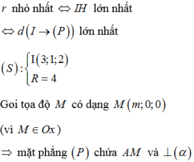
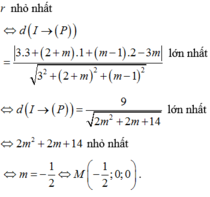
Chọn B
Nhận xét: Cho ba mặt phẳng đôi một vuông góc với nhau (P), (Q), (R) tại I. Hạ AH, AD, AE lần lượt vuông góc với ba mặt phẳng trên thì ta luôn có: IA2 = AD2 + AH2 + AE2
Chứng minh: Chọn hệ trục tọa độ với I(0; 0; 0), ba trục Ox, Oy, Oz lần lượt là ba giao tuyến của ba mặt phẳng (P), (Q), (R). Khi đó A (a; b; c) thì IA2 = a2 + b2 + c2 = d2 (A, (Iyz)) + d2(A, (Ixz)) + d2(A, (Ixy)) hay IA2 = AD2 + AH2 + AE2 (đpcm)
Áp dụng: Mặt cầu (S) có tâm I (1; -1; 2) và có bán kính r = 4;
Gọi Ii và rj là tâm và bán kính của các đường tròn I (1; 2; 3)
Ta có tổng diện tích các đường tròn là: