Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
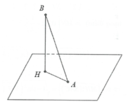
Ta có: d B ; P ≤ A B , dấu “=” xảy ra ⇔ A B ⊥ P
Khi đó n P → = A B → 1 ; - 1 ; 1 ⇒ P : x - y + z - 1 = 0 ⇒ d O ; P = 1 3 .

Ta có Pt d2 :x+2y-5=0
vì M ϵ d1 :x-y-1=0 nên M(m,m-1)
MA2 = (-1-m)2 + (2-m+1)2 = 1+2m+m2 +9-6m+m2 =2m2 -4m+10
<=> MA=\(\sqrt{2m^2-4m+10}\)
d(m,d2 )= \(\frac{\left|m+2m-2-5\right|}{\sqrt{1^2+2^2}}\) =\(\frac{\left|3m-7\right|}{\sqrt{5}}\)
theo bài ra thì MA=d(M,d2)
=>\(\frac{\left|3m-7\right|}{\sqrt{5}}\)=\(\sqrt{2m^2-4m+10}\) <=>|3m-7|=\(\sqrt{5}\)\(\sqrt{2m^2-4m+10}\)
<=>9m2 -42m +49=5(2m2-4m+10)
<=>9m2 -42m +49=10m2 -20m +50
<=>m2 +22m +1=0
<=>m= -11+2\(\sqrt{30}\) hoặc m=-11-2\(\sqrt{30}\)
=> M(-11+2\(\sqrt{30}\) ,-12+2\(\sqrt{30}\) ) hoặc M(-11-2\(\sqrt{30}\) ,-12-2\(\sqrt{30}\) )

a. Số đoạn thẳng vẽ được là : \(C^2_{16}=120\)
b. Số tam giác tạo thành là : \(C^3_{16}=560\)






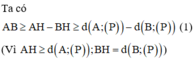

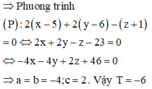
Chọn đáp án D
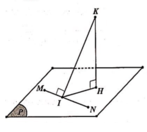
Giả sử mặt phẳng (P) có vectơ pháp tuyến là n ⇀ = a ; b ; c a 2 + b 2 + c 2 ≠ 0 .
Khi đó phương trình mặt phẳng (P) có dạng a x + b y + c z + d = 0 .
Do M 0 ; 0 ; 1 ∈ P nên c + d = 0 ⇔ d = - c
Do N 0 ; 3 ; 1 ∈ P nên 3 b + c + d = 0 ⇔ b = 0
Khi đó P : a x + c z - c = 0
Từ giả thiết ta có d B ; P = 2 d A ; P
⇔ - 2 a + 2 c a 2 + c 2 = 2 a - c a 2 + c 2 (luôn đúng). Vậy có vô số mặt phẳng (P) thỏa mãn.