Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
Gọi \(M\left(x;y;z\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y;-3-z\right)\\\overrightarrow{MB}=\left(-2-x;-y;2-z\right)\end{matrix}\right.\)
\(2\overrightarrow{MA}=\overrightarrow{MB}\Rightarrow\left\{{}\begin{matrix}2-2x=-2-x\\4-2y=-y\\-6-2z=2-z\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=4\\z=-8\end{matrix}\right.\) \(\Rightarrow M\left(4;4;-8\right)\)
2.
Ta có:
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-2;2;-4\right)\\\overrightarrow{AC}=\left(0;1;c-2\right)\end{matrix}\right.\)
Tam giác ABC vuông tại A \(\Rightarrow AB\perp AC\)
\(\Rightarrow\overrightarrow{AB}.\overrightarrow{AC}=0\)
\(\Rightarrow-2.0+2.1-4\left(c-2\right)=0\)
\(\Rightarrow c=\dfrac{5}{2}\)
Vậy \(C\left(1;0;\dfrac{5}{2}\right)\)

Chọn B
Mặt phẳng (ABC) đi qua B (1; 0; -1) và có một véctơ pháp tuyến là:
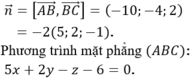
Phương trình mặt phẳng (ABC): 5x + 2y - z - 6 = 0
Độ dài đường cao xuất phát từ đỉnh D (0; 0; d) của tứ diện ABCD bằng d(D, (ABC))
Theo bài ra ta có:
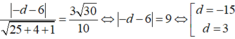
Do D thuộc tia Oz nên D (0; 0; 3).

Đáp án là D.
+ Gọi H(x;y;z) là chân đường phân giác trong góc A của ∆ ABC
Ta có:
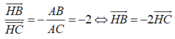
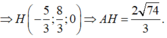
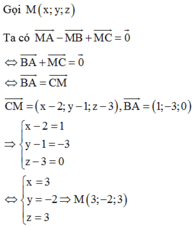
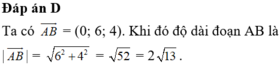
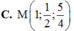
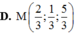
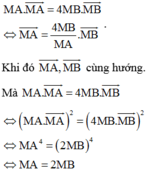




Đáp án B