Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi G (2;2;-2) là trọng tâm tam giác ABC, khi đó ![]()
Ta có:
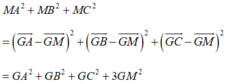
đạt giá trị nhỏ nhất khi M là hình chiếu vuông góc của G trên mặt phẳng (P). Khi đó tọa độ của M (a;b;c) và vecto ![]() cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ
cùng phương với vecto pháp tuyến n (1;-2;2) thỏa mãn hệ 
Vậy a+b+c=3.

Đáp án A
Phương pháp
+) Gọi I là điểm thỏa mãn hệ thức I A → + I B → + 3 I C → = 0 → tìm tọa độ điểm I.
+) Chứng minh M A 2 + M B 2 + 3 M C 2 nhỏ nhất <=> MI nhỏ nhất.
+) MI nhỏ nhất <=> M là hình chiếu của I trên (P)
Cách giải
Gọi là điểm thỏa mãn ta có hệ phương trình:

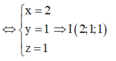
Ta có:
![]()
![]()
![]()
![]()
![]()
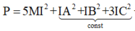

![]()
Khi đó M là hình chiếu của I trên (P)
Gọi d là đường thẳng đi qua I và vuông góc với (P)

![]()
M ∈ (P) Suy ra
=> 3(3t+2) - 3(-3t+1)-2(-2t+1)-12=0
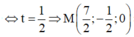
=> a+ b+ c =3

Đáp án A
Gọi I là điểm sao cho
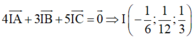
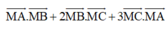
![]()
![]()
![]()
![]()
![]()
![]()
![]()
khi và chỉ khi M là hình chiếu của I lên mặt phẳng (Oxy)
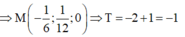
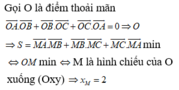
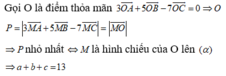
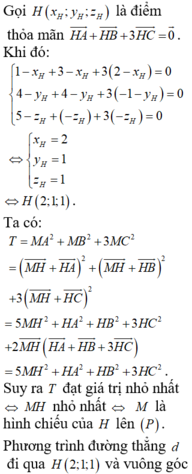

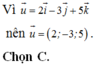




Đáp án B.