Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn A
Mặt phẳng qua I vuông góc với d có phương trình
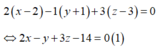
Gọi H là hình chiếu của I trên đường thẳng d.
Thay x, y, z từ phương trình của d vào (1) ta có
Chọn A
Gọi (P) là mặt phẳng đi qua A và vuông góc với đường thẳng d.
Phương trình của mặt phẳng (P) là:
1(x - 3) + 2 (y - 2) + 2(z - 0) = 0 <=> x + 2y + 2z - 7 = 0
Gọi H là hình chiếu của A lên đường thẳng d, khi đó H = d ∩ (P)
Suy ra H ∈ d => H (-1 + t; -3 + 2t; -2 + 2t)
mặt khác H ∈ (P) => -1 + t - 6 +4t -4 + 4t - 7 = 0 => t = 2. Vậy H (1;1;2)
Gọi A' là điểm đối xứng với A qua đường thẳng d, khi đó H là trung điểm của AA' suy ra A' (-1; 0; 4)
Chọn A
Vì A thuộc 
nên A (1+2t;1-t;-1+t).
Vì B thuộc 
nên B (-2+3t';-1+t';2+2t').
Thay vào (3) ta được t=1, t'=2 thỏa mãn.
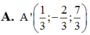
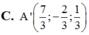
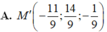
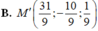
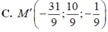
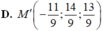
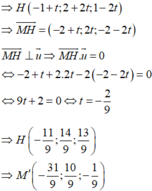
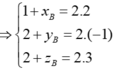
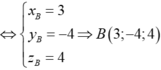
Đáp án C.
Đường thẳng d có véc tơ chỉ phương u → ( 2 ; 2 ; - 1 )
Gọi H(1+2t ;-1+2t ;-t) ∈ d là tọa độ hình chiếu vuông góc của A trên d.
A’ đối xứng với A qua d ⇔ H là trung điểm của AA’