Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

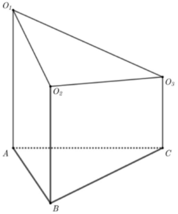
Gọi O1, O2, O3 lần lượt là tâm của ba mặt cầu đã cho và bán kính tương ứng là x, y,z ta có điều kiện các mặt cầu đôi một tiếp xúc ngoài là 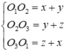 và điều kiện tiếp xúc với mặt phẳng
và điều kiện tiếp xúc với mặt phẳng
(ABC) là 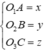
Vậy theo pitago có
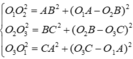
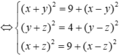
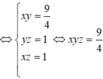
Chọn đáp án A.

Đáp án B
Giả sử (P) tiếp xúc với (S1), (S2) lần lượt tại A,B

Ta có:
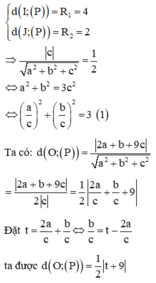

Suy ra M + m = 9.

Đáp án C
Do IJ = 4 > R 1 + R 2 nên hai mặt cầu cắt nhau
Giả sử IJ cắt (P) tại M ta có M J M I = R 2 R 1 = 2
=> J là trung điểm của MI
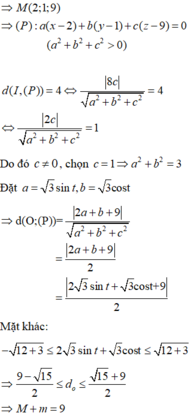

Đáp án C
Do IJ =4 > R 1 + R 2 nên hai mặt cầu cắt nhau
Giả sử IJ cắt (P) tại M ta có M J M I = R 2 R 1 = 2 => J là trung điểm của MI
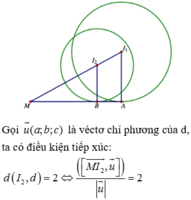
=> M(2;1;9) => (P): a(x-2)+b(y-1)+c(z-9)=0 a 2 + b 2 + c 2 > 0
d(I,(P))=4 ⇔ 8 c a 2 + b 2 + c 2 = 4 ⇔ 2 c a 2 + b 2 + c 2 = 1
Do đó c ≠ 0 , chọn c=1 => a 2 + b 2 = 3
Đặt a = 3 sin t , b = 3 cos t ⇒ d ( O ; ( P ) ) = 2 a + b + 9 a 2 + b 2 + c 2 = 2 a + b + 9 2 = 2 3 sin t + 3 c o s t + 9 2
Mặt khác
- 15 ≤ 2 3 sin t + 3 cos t ≤ 15 ⇒ 9 - 15 2 ≤ d 0 ≤ 9 + 15 2 ⇒ M + m = 9

Ta dễ thấy ba điểm A, B, C thuộc mặt phẳng ![]() , 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
, 3 mặt cầu là ở ngoài nhau. Mỗi mặt phẳng tiếp xúc với hai mặt cầu thì sẽ có hai tình huống.
1. Cả 3 mặt cầu ở cùng một nửa không gian chia bởi mặt phẳng tiếp xúc. Có 2 mặt phẳng như vậy.
2. Mặt phẳng tiếp xúc chia 2 mặt cầu về một phía và phía còn lại chứa mặt cầu kia. Có 4 mặt phẳng tiếp xúc chia mặt cầu lớn và mặt cầu nhỏ ở cùng một bên. Có một mặt phẳng tiếp xúc chia 2 mặt cầu nhỏ về một bên (ở đây do R + r + d ( A, BC ) nên mới tồn tại 1 mặt phẳng tiếp xúc theo yêu cầu, nếu R + r + d > d ( A, BC ) thì sẽ tồn tại 2 mặt phẳng tiếp xúc)
Đáp án cần chọn là B



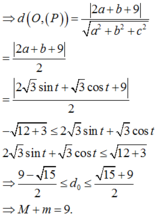

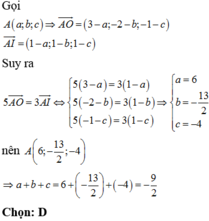
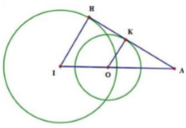

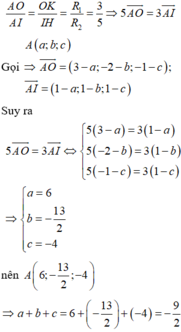
Gọi I1, I2, R1, R2 lần lượt là tâm và bán kính của các mặt cầu (S1) và (S2). Theo điều kiện tiếp xúc có I 1 A = R 1 ; I 2 B = R 2 .
Mặt khác hai mặt cầu tiếp xúc ngoài với nhau tại điểm M nên I 1 I 2 = R 1 + R 2 = I 1 A + I 2 B ⇒ I 1 I 2 luôn tiếp xúc với mặt cầu đường kính AB tại điểm M tức là M thuộc mặt cầu đường kính AB
Phương trình mặt cầu đường kính AB là ( S ) : x 2 + y - 1 2 + z - 2 2 = 9 có tâm I(0;1;2), R = 3.
Vì vậy M ∈ ( S ) ⇒ d M , P ≤ d I , P + R
=672+3=675.
Gọi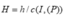
Dấu bằng đạt tại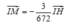
Chọn đáp án A.