Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{b}-1=\dfrac{c}{d}-1\Rightarrow\dfrac{a-b}{b}=\dfrac{c-d}{d}\)
\(\Rightarrow\dfrac{b}{a-b}=\dfrac{d}{c-d}\Rightarrow\dfrac{2b}{a-b}=\dfrac{2d}{c-d}\)
\(\Rightarrow\dfrac{2b}{a-b}+1=\dfrac{2d}{c-d}+1\)
\(\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\) (đpcm)

Áp dụng dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{e}=\frac{e}{g}=\frac{a+b+c+d+e}{b+c+d+e+g}\)
=> \(\left(\frac{a}{b}\right)^{404}.\left(\frac{b}{c}\right)^{404}.\left(\frac{c}{d}\right)^{404}.\left(\frac{d}{e}\right)^{404}.\left(\frac{e}{g}\right)^{404}\)
\(=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}.\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404}\)
=> \(\left(\frac{abcde}{bcdeg}\right)^{404}=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{404+404+404+404}\)
=> \(\frac{a^{404}}{g^{404}}=\left(\frac{a+b+c+d+e}{b+c+d+e+g}\right)^{2020}\)

a: Xét ΔABD và ΔEBD có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc BED=góc BAD=90 độ
=>ΔBED vuông tại E
c: AD=DE
DE<DC
=>AD<DC
d: AB+EF=BE+EF
mà BE+EF>BF
nên AB+EF>BF

hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)

+) Ta có: \(\dfrac{a}{b}< \dfrac{c}{d}\Rightarrow\dfrac{ad}{bd}< \dfrac{bc}{bd}\Rightarrow ad< bc\)
( do b, d > 0 )
+) Ta có: \(ad< bc\)
\(\Rightarrow\dfrac{ad}{bd}< \dfrac{bc}{bd}\Rightarrow\dfrac{a}{b}< \dfrac{c}{d}\left(b,d>0\right)\)
Để \(\dfrac{a}{b}< \dfrac{a+c}{b+d}\) thì \(a\left(b+d\right)< b\left(a+c\right)\Leftrightarrow ab+ad< ab+bc\Leftrightarrow ad< bc\Leftrightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
Để \(\dfrac{a+c}{b+d}< \dfrac{c}{d}\) thì \(\left(a+c\right).d< \left(b+d\right).c\Leftrightarrow ad+cd< bc+cd\Leftrightarrow ab< bc\Leftrightarrow\dfrac{a}{b}< \dfrac{c}{d}\)
Chúc Bạn Học Tốt !!!Đạt nhiều thành tích trong học tập
Xem lại đề nha bạn :\(\dfrac{a}{b},\dfrac{c}{d}\left(b,d>0\right)\) chứ

Thay b^4=(ac)^2 và tương tự với d^4
Từ đó đặt thừa số chung và sẽ ra kết quả!
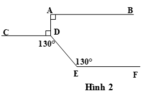
Ta có: A B ⊥ A D ; C D ⊥ A D (gt).
Þ AB // CD (vì cùng vuông góc với AD) (1)
Ta lại có: C D E ^ = E ^ = 130 o (gt)
Þ EF // CD (vì có cặp góc so le trong bằng nhau). (2)
Từ (1) và (2) Þ AB // EF (vì cùng song song với CD).